36Hint : 600 plays an important role............
he ha ha
This is a good prob from my Xth mathematika... and so i thought of sharing it with u all...
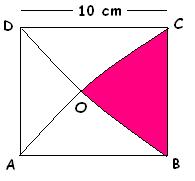
ABCD is a square with each sides equal to 10 cm and in which ABC and BCD are the quadrants where arcs BD and AC intersect at O. Calculate the area of the shaded region.
Note : Belongs to HOTS [high order thinking skills] category....
-
UP 0 DOWN 0 0 2
2 Answers
1
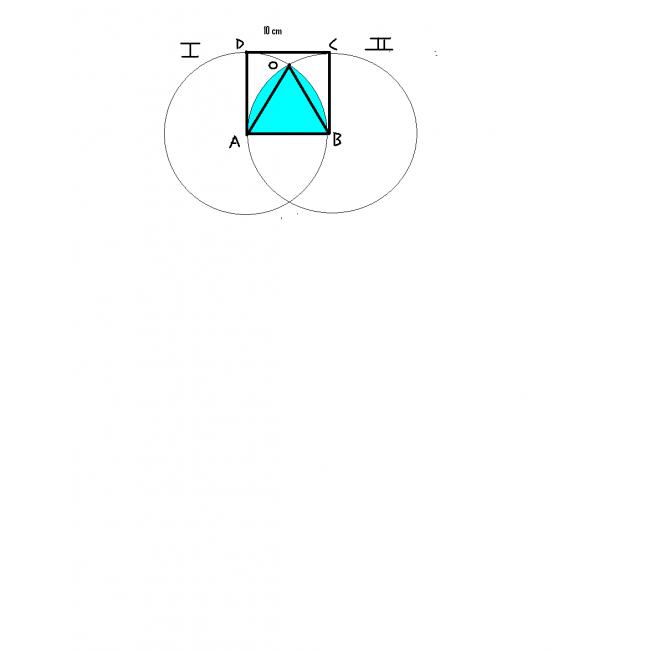
Circles I and II are formed from the given quadrants,with centers A and B.
ΔABC is equilateral.
area(ABC)=√3/4*100=25√3
Now let's take a closer look at one circle...say circle I.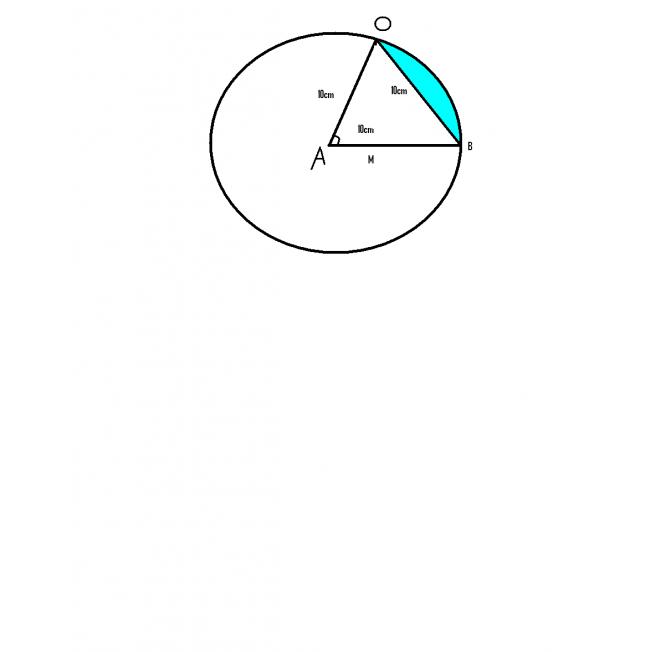
AO=BO=AB=10cm
Since both the circles are equal their sectors will also be equal.
angle OAB=60°
Area of sector enclosed by AOB= Π*AB*AB*(60°/360°)
= Î *100/6
Area of ΔABO=25√3
Area of shaded sector enclosed by OB=(Π*100/6)-(25√3)
Area of total shaded region=(25√3)+2{(Π*100/6)-(25√3)
=(Π*100/3)-25√3
=61.4 sq.cm.(approx.)