What is the area of the shaded region?

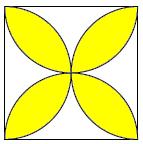
area of 4 semicircles = \pi=area of square + area of shaded part
so area of shaded part = \pi -1

fibonacci.....this is 9-10 maths yaar........:-)

firstly we numbering the regions , white region is called region A and yellow called B ..

SOLUTION

let the side of the suare is a then the radius become a/2 ..

remaining total area of REGION( A) = 2*(a*a - 2*pi/2*a*a/4) = x (let)

so for yellow area REGION (B) = a*a -x ,

final answer is =pi*a*a -a*a

@ aveeek....fibonacci is in 10th class only [1]

Let the shaded portions be marked as 'a' and the unshaded portions as 'b'

Now, we have two equations

4a + 4b = 1 ------- (i)

2a + b = pi/2 ------ (ii)

on multiplying eqn. (ii) by 4 we have,

8a + 4b = 2pi ------ (iii)

On substracting eqn. (i) from (iii) we get,

so, 4a = 2pi - 1

or, a = (2pi - 1)/4

So, total area of shaded regions = 4a = 4 x (2pi - 1)/4 = 2pi - 1 Ans...!!