There is a n-sided regular polygon having n number of vertices.
I randomly choose a line segment joining any 2 vertices of the polygon.
What are my Chances that it is a diagonal of the polygon.
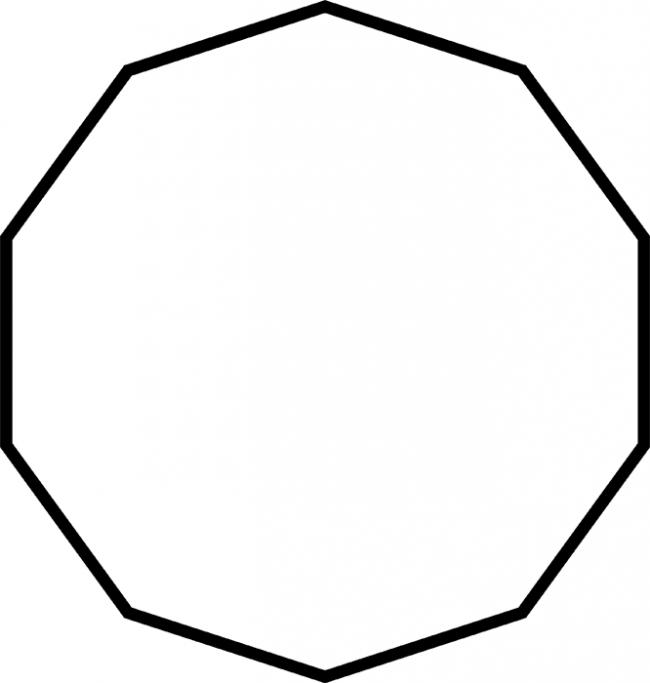
I hope that the question is clear.:-)
-
UP 0 DOWN 0 1 3

3 Answers
diagnol in sense ????and the n sided polygn doesnt have and polygons u see.....and joining any 2 of them can give u a diagnol.........
Think of it to be a polygon having only the vertices without any lines joining them.
Then if I randomly chose a line then it can be a side of the polygon as well as a diagonal.
For eg.
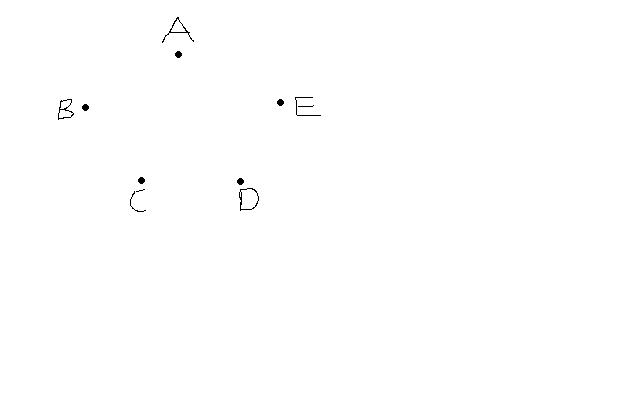
In the above picture ,which was once a regular 5-sided polygon (perhaps it is called a pentagon):
A line can be drawn from A to E (which would be a side of the polygon) and
A line can also be drawn from A to D (which would be a diagonal of the polygon)
What r my chances that it is a diagonal?
we can choose any two points by n(n-1) ways but choosing 1 and then choosing is equivalent to choosing 2 and then 1
so the real no of ways=n(n-1)/2
now the 2 points to be diagonal vertices, the vertices should not be adjacent thus if we choose one point 3 points cannot be chosen, 1 the point itself and 2 other points in its nearest vicinity...
thus number of ways=n(n-3)/2
thus, chances of getting diagonal vertices is n-3n-1