1option d >> 4/3
1) If \alpha, \beta, \gamma and \delta are the angles made by a line with the diagonals of a cube, then cos^2\alpha +cos^2\beta +cos^2\gamma +cos^2\delta is equal to :
(a) 0
(b) 1
(c) 2/3
(d) 4/3
-
UP 0 DOWN 0 0 14
14 Answers
112) The sum of distances of (1,-1,-1) from the axes is
(a) 3√2
(b) 2√3
(c) √3
(d) √6
I think the answer is 3......problem is, it is not among the options [2]
11bhaiya, (1,-1,-1) is at a distance of 1 from each axis....so sum of distances is 3, right?
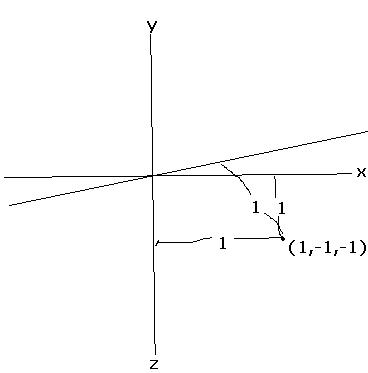
62Think again! what is the distance of th epoint (1,1,1) from line x axis?
1Maybe u got confused by drawin it 2 dimensionally. Try imaginin it it 3D. The distances of the point from 2 of the axes won't be 1 unit.
113) The equation of the line x-y+2z=5, 3x+y+z=6 in symmetrical form is?
4) The equation of the plane passing through the intersection of the planes z-2y+z+4=0 and 4x+y+2z+1=0 is?
5) The shortest distance of the point (2,-4,4) from the plane r.(3i-j+4k)=0 is
(a)7
(b)√21
(c)2√21
(d) 1
13rd wud be a bit lengthy sort i mean im feeling too lazy to do it now
4th well there can be many many planes passing thru their line of intersection
in fact there will be a family of planes given by P1 + k P2 =0
which should represent diffnt planes for diffnt k (except P2 that is)
and please check the eqn of the 1st plane is it x-2y ??
1according to me in 5th question (im not 100 percnt sure )
the equation is same as 3x -y + 4z =0
now we can solve it
♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫♫