11@ Mr.Kalyan
check post #21 by ankit[1]
1)
A ray of light is coming along the line
y = b
from the positive direction of x axis and strikes a concave mirror whose intersection with xy plane is a parabola
y2 = 4ax .
If a and b are positive, then the equation of the reflected ray is :
(a) y-2ab=\frac{2b}{b^2+1}(x-ab^2)
(b) y-2ab=\frac{2b}{b^2-1}(x-ab^2)
(c) y-2ab=\frac{-2b}{b^2-1}(x-ab^2)
(d) None\; of\; these
-
UP 0 DOWN 0 1 34
34 Answers
14) If x2 − x +1 = 0 then value of x3n is :
x = -ω , - ω2
(a) -1,1
is correct
11
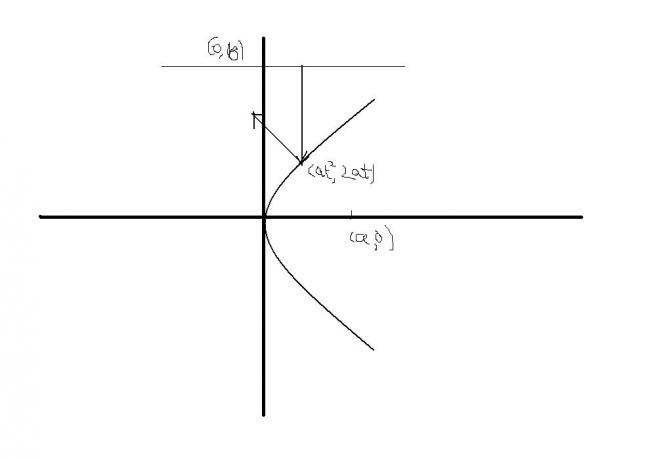
dekh bhai
let the point the parabola be (ab2,2ab)
and it is clear that u have to find the equation of the reflected ray
so,
y-2ab=m(x-ab2)
now we have to find its slope
u have to know that the ray would pass through the focus of the parabola
i.e(a,0)
now u have 2 points
find their slope
their slope is 2ab-0/ab2-a
=2b/b2-1
so the equation becomes
y-2ab=2b/b2-1(x-ab2)
1Is da ans to the 4th Q a??
x is e^i'pi/3 or e^-i'pi/3
x^3 = e^i'pi or e^-i'pi both meaning the same
So x^3n= e^i'npi = 1, -1
1yaar itna nautanki kyun karte ho .. u know the ray will pas thro' focus so (a,0) is satisfied .. put it in the 3 options only one is satisfying :)
1limitz wala u can also do like first rationalize
so ur q is
lim x→infi (-x)/(x+√x^2+x
so nw divide thruout by x
u get ur answer as -1/2
1How can you say that the ray passes through the focus.
This mirror is parabolic, and not spherical.
We need to take the normal at (b2/4a,b)
And make <i = <r
We get the slope of the reflected ray
And equation thru slope point form.of line
1oye, this a a property of parabolic mirror .. check it out in wikipedia if u don't believe ......
62kalyan, this is a standard result. It is one of the must knows!
11\int \frac{xsin^{-1}xdx}{\sqrt{1-x^2}} = \int x \;d\left(\frac{(sin^{-1}x)^2}{2} \right) = x\frac{\left(sin^{-1}x \right)^2}{2}-\int \frac{(sin^{-1})^2}{2}}dx Got the answer....but is this step right (I'm asking for all problems which end up like this)??
11Ani ......
yaar do this question b parts
iss mein mushkil kya hai
their method is not wrong but is difficult to understand (u can verify both the results )
take x/√1-x2 as the 2nd f(x) and sin-1x as the 1st f(x)
and substitute x=cos@ and dx=-sin@d@ to solve it and u will reach to ur answer [1]
113)
\int \frac{dx}{sin^6x + cos^6x}
(a)tan^{-1}(tanx-cotx)+ c
(b) -tan^{-1}(-2cot2x)+c
(c) log(tanx-cotx)+c
(d) log(cotx-tanx)+c
11i couldn't understand the options for this question:
4) If x2 − x +1 = 0 then value of x3n is :
(a) -1,1
(b)1,0
(c)-2,2
(d)0,2
112)
limx-->∞ x-√(x+1/2)2-1/4
now i hope its clear
√(x+1/2)2-1/4 --------> x+1/2 as x tends to ∞
so answer must be -1/2
11Sorry mani....i'm weak in limits
Why shd √(x+1/2)2-1/4 ----> ∞ as x ----> ∞ ???
1hw can the answer be -1/2 manipal............is the √-1/4=-1/2.........tusii great hoo yaar...
112)
\lim_{x\rightarrow \infty}\left[x-\sqrt{x^2+x} \right]
(a)1/2
(b)1
(c)-1/2
(d)0
113)
HINT :
sin6x+cos6x=(sin2x)3+(cos2x)3
=1-3sin2xcos2xdx
divide numerator and denominator by cos4x
convert it into tan and sec functions
do the required substitutions and i hope u will be able to olve it
in case of doubts
do ask again[1]