1Yes,the answer is indeed 2Ï€.
Circle x2+y2=1 subtends angle θ on a varible point P such that π3<θ<π2 then the area of region generated by locus of point P is:
-
UP 0 DOWN 0 0 3
3 Answers
1
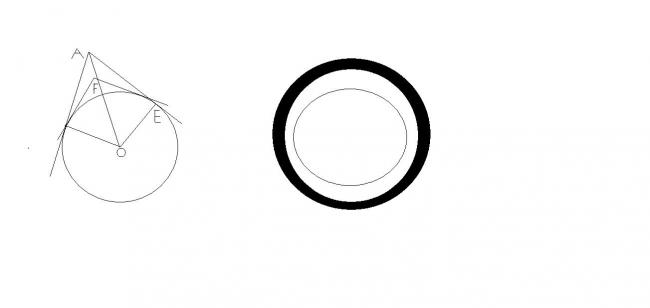
I have denoted , by " A " , the point which subtends an angle of " π3 " at the center of the circle ( " O " ) , and by " F " , the point which which subtends an angle of " π2 " .
Clearly , the loci of the points are 2 circles , each of radius " AO " and " FO " respectively .
Since , Angle ( AOE ) = 30 ° , hence , " AO = OE sec ( 30 ° ) = 2 "
Simalarly , " FO = √ 2 " .
Hence , the required area of the region is the region ( see picture ) contained in between these circles , which is : -
Area = Ï€ ( 2 2 ) - Ï€ ( √ 2 ) 2 = 2 Ï€