L/sinB = AB/sinP (triangle APB)
AB/sin(180-P) = R/sin(90-B) (triangle QAB)
tan(P/2) = R/L (if you join PQ then triangle PAQ)
using these three u can eliminate B and P and hence get what you want
I Cannot Prove the following:
Please help me to Prove It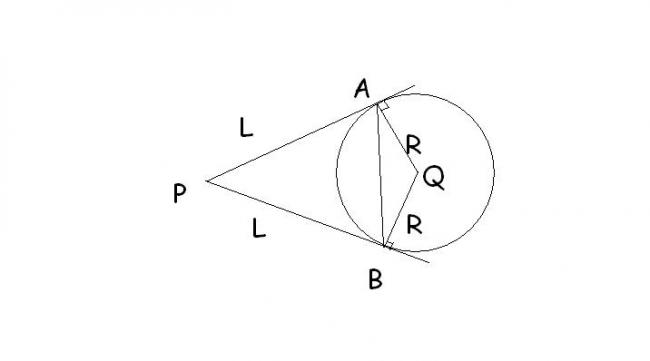

How to Prove These Results ??
Thanks I Advance (If you solve it !!)
L/sinB = AB/sinP (triangle APB)
AB/sin(180-P) = R/sin(90-B) (triangle QAB)
tan(P/2) = R/L (if you join PQ then triangle PAQ)
using these three u can eliminate B and P and hence get what you want
Too easy....
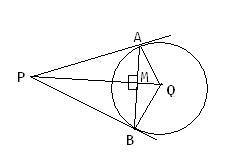
Join PQ which meets AB at M
clearly, triangle BPM and APM are congruent by SAS criterion...
=> LPMA = 90°
Now, In triangle APQ we have,
AP = L and AQ = R, LQAP = 90°, => PQ = √(L2 + R2)
Thus, 1/2 x AQ x AP = 1/2 x PQ x AM [both equal to area of triangle APQ]
=> AQ x AP = PQ x AM
=> AM = AQ X AP / PQ = R x L / √(L2 + R2)
or, AM = R x L / √(L2 + R2)
But, AB = 2 AM
=> AB = 2RL /√(L2 + R2)
---------------------------------------------------------------------------------------------
Now comes the area of triangle ABP
So do this,
since, AM = RL / (L2 + R2) and AQ = R and LAMQ = 90°
So by pythagoras' theorem we find QM and then subtract it from PQ to find PM
i.e., PM = [√(R2 + L2) - R2/√(R2 + L2)] = L2/√(R2 + L2)
Thus, Area of triangle ABP = 1/2 x AB x AM = 1/2 x 2RL/√(R2 + L2) x L2/√(R2 + L2)
or, Area of triangle ABP = RL3/(R2 + L2)
Hope this helps u...!!
You did this
So by pythagoras' theorem we find QM and then subtract it from PQ to find PM
why find QM then Subtract it from PQ
we can directly find PQ = √[(AP)2 - (AM)2]
JUST POINTING OUT !!!!
THANKS AGAIN
@Ironman -> For ur second last post.... don't worry... i m the most stupid person.... so u still have someone... who is even more stupid than u r...!!
now this is four ur above post....
you r 100% right....!!
actually i m fool at times.....
we could've directly found, PM by PM = √(AP2 - AM2)