This sum is actually quite easy.....
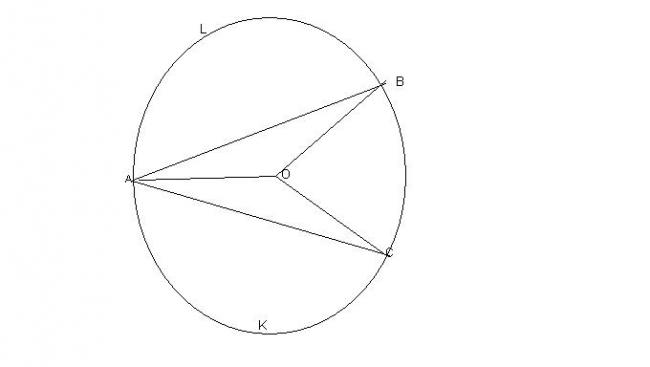
See let angle BAc be 2\theta and If O be the centre of the circle then Join AO, OC, and OB.
Look at arc ACK.....area of which is basically AREA OAC-AREA of triangle OAC......
Similarly for arc ALB....
\frac{180-2\theta}{2\pi}.\pi r^2 -\frac{1}{2}r^2sin2\theta =\frac{4\theta}{2\pi}\pi r^2+(r^2sin2\theta) r cancells out!
Now get all the terms to 1 side to have f(\theta)=0 - hopefully no calculation mistakes......though I get the feeling i've made some!
A is a point on circumference of a circle, chords AB and AC divide circle area in three equal parts, f(x)=0 is an equation whose root is angle BAC, then f(x) is equal
(A) x-sinx+\pi3
(B) x+sinx+\pi3
(C) 2[x-sinx+\pi3]
(D) 2[x+sinx-\pi3]
-
UP 0 DOWN 0 1 7

7 Answers
I will give a hint to go around this one..
First B and C will be symmetric about the diameter passing through A
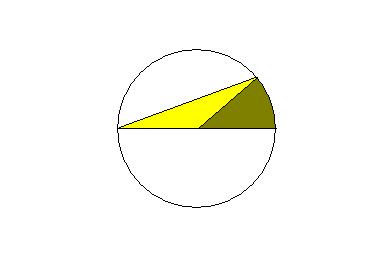
Now find the area of the yellow + area of golden part... (That should be 1/6th the area of the circle)
Angle of golden part is 2 times area at the yellow part (center and circumference)
Area will be θ/2 r2 + r. r sin θ = pi r2/ 6
θ/2 + sin θ = pi 6
So the answer is D
Nishant sir, have i erred somewhere? I've been typing for a long time, so didn't see ur post coming.....
thanks to both of you...
" θ/2r2 + 1/2r2sinθ = pi r2/6 "
i made a mistake in formula...took 360 as pi rather then 2pi...!!!!!!!!!!!!!
AAre I took it as 2 theta, and BOC as 4theta.......That should also giv na......Better replace 2 theta in my soln as k.....