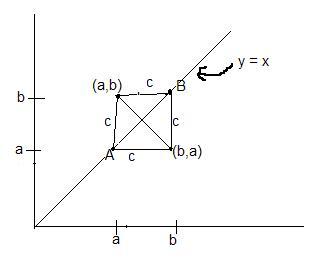koi badhiya uapy to nahi dikh raha :(
find the length of the common chord of two circles:
(x-a)2+(y-b)2=c2 and (x-b)2+(y-a)2
a) √4c2-2(a-b)2
b) √4b2-2(a-c)2
c) √2c2-2(a-b)2
d) √2c2-2(c-b)2
-
UP 0 DOWN 0 0 22

22 Answers
OH k... Yah!!!
Sorry wasnt tuff at all especially after lukin at Sir's expression[6]
SKY: compare wid ur diag.
x=PD, r = MP; 2r2 = PN2
now jus pyhtagoras
eqn of chord of contact:
x - y = c2/2(a-b) => PQeqn.
MD = perpendicular distance of (a,b) from PQ
= |a-b - c2/2(a-b)| /√2
now,
PD2 = PM2 - MD2
= c2 - |a-b - c2/2(a-b)|2 /2
= [kuchh kuchh]
so PD = √[kuchh kuchh]
hence length of the chord = 2PD = 2X√[kuchh kuchh]
this is not that tough!
\sqrt{r^{2}-x^{2}}+\sqrt{2r^{2}-x^{2}}=\sqrt{(a-b)^{2}+(b-a)^{2}}
solve for x
2x will give the length fo the chord
OKie, I'll giv u an eg.
FIND DA LENGTH OF COMMON CHORD B/W da fol 2 circles :
(x-a)^2+(y-b)^2=c^2 and (x-b)^2+(y-a)^2 = 2c^2
[2]
RK, tumhari methd mein is change ko koi scope hai?
lagta hain ab sir ko hi puchhna padega
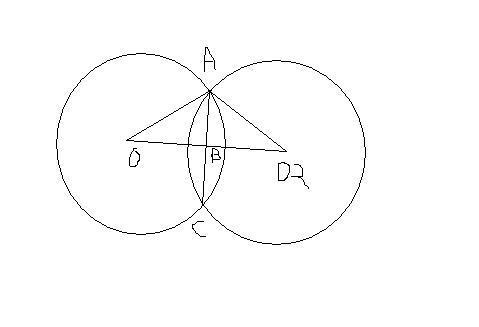
OO2=((a-b)2+(b-a)2)1/2=√2(a-b)
OB=OO2/2=(a-b)/√2
OA=c
AC=2AB=2(OA2-OB2)1/2