Conic

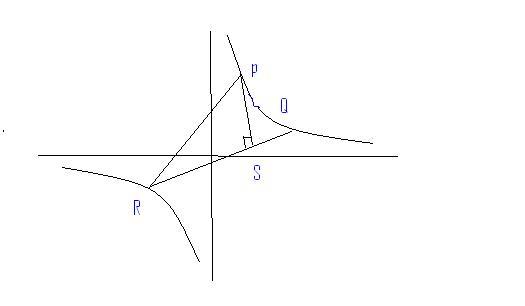
Prove that for any triangle inscribed in a rectangular hyperbola its orthocenter also lies on that same rect hyperbola

2 Answers

let three points be p,q,r

their coordinates are t₁,t₂,t₃

slope of qr is -1t₂t₃

thus slope of PS IS t₂t₃

EQUATION OF PS IS t₁y-C=xt₁t₂t₃-ct²₁t₂t₃

similarily EQUATION OF QT IS t₂y-C=xt₁t₂t₃-ct1t²₂t₃

solving these two we get orthocentre as (-ct₁t₂t₃,-ct₁t₂t₃) which lies on xy=c²

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω