1b)-3
maximum length of perpendicular from centre of ellipse x2/9+y2/4 =1 on any normal to this ellipse is equal to a+5, then value of a is
a. -4 b. -3
c. 4 d. none
-
UP 0 DOWN 0 0 6
6 Answers
1maximum length of perpendicular from centre of ellipse x2/9+y2/4 =1 on any normal to this ellipse is equal to a+5, then value of a is
if u r asking 4 the maximum length then
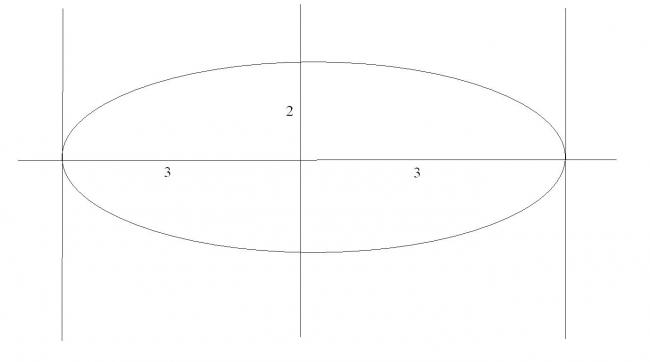
a+5=3
a=-2
check ur question again or the sorce if u have any doubts but the produre to be followed id this
1lonely it is the max distance from the centre to the tangent
check it out...............
1use normal form of the equation xasec - bcosec y = a2-b2
use distance from origin and maximise it
u will get ur results