111)B
2)B(not sure)
1]A ray of light is sent along the line 2x-3y+4=0 ,upon reaching the line x+2y-7=0,the ray is reflected from it. The slope of the line containing the reflected ray is equal to
A. 5 B. -18 C. -15 D. 20
2]Consider the circle c1: x2 +y2 -6x-8y+15=0 , c2: x2 +y2 -6x-8y+20=0 , now from any point P on c1 , pair of tangents PA and PB are drawn on c2, the locus of the ortho centre of triangle PAB is
A. x2 +y2 -6x-8y+20=0 B. x2 +y2 -6x-8y+10=0 C. x2 +y2 -6x-8y+5=0
D. none
-
UP 0 DOWN 0 0 5
5 Answers
11Q2)
Ans : D (very sure)
c1 & c2 are concentric.
Now r1 = √10 & r2 = √5
r1 = (√2) r2
Thus c1 is the "director circle" (locus of intersection pts. of perpendicular tangents) of c2 .
So Λ PAB is always right angled at P
Thus reqd locus is c1 itself ie. x2 +y2 -6x-8y+15=0
1as we draw two tangents from the external point, the chord of contact will be the third side. so one altitude will be from that point to third side.
as orthocentre is point of concurrence of all three altitudes ,we already know one altitude so the orthocentre will along that line.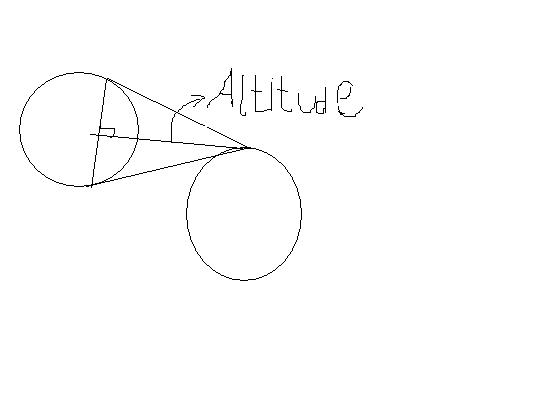 
1!st sum
let d slope of incidnt line be m
slope of refcltd line be m'
nw ........d line perpndicular to d line frm wich reflction takes place .....ie d normal ...will make equal angles wid these line of slope m and m'so u can do
by euqatin d slopes ie @
tan@=mod (m-m')/(1+mm')
u'll get d answer
1what chandu is telling ? are the circles not concentric, if yes then his proposition is wrong, thus C1 is the director circle .... not understood ,please explain.
