doubt( help me out.)

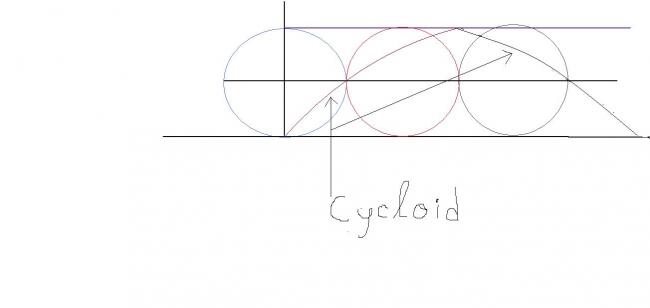
Well , the curve described by a point lying on the circumference of a circle if the circle is rolling upon a straight line is called a CYCLOID .

Its parametric equation is , X = a ( z - sin z ) And Y = a ( 1 - cos z ) Where a is the radius of the circle and z is the angle which is shown in the figure as angle PAB . A is the center of the circle .

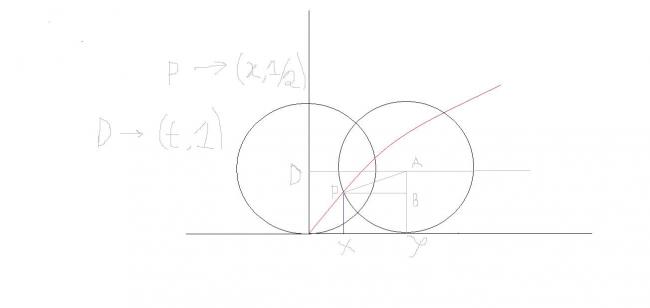
From your question , a = 1 cm . Suppose the point ( x , 1 / 2 ) is P .

According to the parametric equations ,

Y = 1 ( 1 - cos z ) = 1 / 2 , for the point P .

So t = pi / 3

Hence x for the point P = z - sin z = pi / 3 - sin ( pi / 3 ) = Ans

Oh , and I forgot to add that the circle can only roll towards +ve X - axis as t is given increasing .

I was going through my previous posts when I found out this one , a beauty . I tried to solve it another way , and goodness me , I found out a much simpler solution . Hope you like it -

Point X - { t , 1 } , i . e , center of the circle ;

Point A - { x , 1 / 2 } , whose x - co ordinate is to be found .

Point Y - { 0 , 1 / 2 } ,

Point O - { x , 0 } ,

XY = YZ = AO =1 / 2 { I am talking about distances }

XZ = 1 , AX = 1 { radius given 1 }

First , you should realize that the x - co ordinate , which we want to find , is ,

x = Length of arc AZ - Length of line AY ; ........................1

Now , from the triangle XYA ,

cos d = XY / AX = 1 / 2 ;

Hence , d = Î / 3 ;

Hence , length of arc AZ = R d { where R is the radius }

= { Î / 3 } . 1 ...............2

Again , sin d = AY / AX = AY ;

So , AY = √3 / 2 , ........................3

Hence , from 1 , 2 , and 3 ,

x = { Î / 3 } - { √3 / 2}

yes gallardo that was amazing [1][1][4][5]