1thnx fibonacci...... :)
this question was based on PROPERTIES OF ElLiPsE
if (9,23) and (49,53) are the 2 focii of an ellipse. and x- axis is tangent to it.then find the length of major axis.??
-
UP 0 DOWN 0 0 9
9 Answers
6ae = 25 ( from the condn. )
now write the eqn for tangent to ellipse
equate it to y=0......
u'll get a and b....
1long but correct soln
though 'a' has no meaning since the given ellipse is non standard, it is used for convenience.
the center of the ellipse is (29,38)
we have ae=25
also using the property : if SY and SY' be the perpendiculars from the foci upon the tangent at any point P of the ellipse, then Y and Y' lie on the auxiliary circle and thus OY=OY'=a2 where O is center of the ellipse
here since x axis is tangent, Y is (9,0) and Y' is (49,0) so a2 is 202+202 or a is 20√2
hence e is 5√2/8
it is easy to find the directrix of the ellipse using the fact that it is perpendicular to the directrix and at a distance of a/e from the center.(you can find it by using parametric eqn of a line)
then to get the ellipse, use the definition: distance from focus = e(distance from directrix)
the data given is untidy otherwise can be easily solved :)
1
11
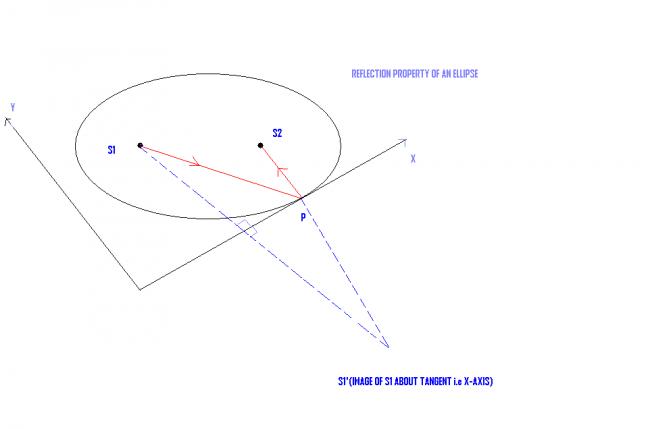
Using reflection property of ellipse i.e a ray of light passing through one focus should pass through the other after reflection. So find S1' i.e image of S1 about x-axis i.e the tangent here. Thus find the eqn of the line S2PS1' and solve it with y=0 to get P.
Now, S1P + S2P =2a.(That is the length of major axis)
21Alternative(though almost same as fibonacci's )
There is another property of ellipse.
THE PRODUCT OF LENGTHS OF PERPENDICULARS DRAWN FROM TWO FOCIS TO ANY TANGENT TO THE ELLIPSE IS SQUARE OF THE SEMI MAJOR AXIS.
Using it we also get it.
1Hi, "nasiko".
I notice your post states, "THE PRODUCT OF LENGTHS OF PERPENDICULARS DRAWN FROM TWO FOCIS TO ANY TANGENT TO THE ELLIPSE IS SQUARE OF THE SEMI MAJOR AXIS."
However, in a previous post in this forum, you ask to prove that the product equals b, which I had assumed was the semi-minor axis (whereas a is the semi-major axis):
[url=http://www.targetiit.com/iit-jee-forum/posts/ellipse-18592.html]ELLIPSE Post[/url]
Which one is correct?
And did you ever get the proof you were seeking?
1Oops, actually I mis-copied it. Your other post did say b2.
However, I am wondering if it should have actually said a2.