help!!!!! sum 1 ...
an ellipse has major axis and minor axis lengths as 2a , 2b
let the foci be x1,y1 and x2,y2
and h,k be its center
and if it slides between co-ordinate axes such that it touches the x and y axis at all times
i)find the locus of one of the foci
ii)find the locus of the center
iii)the locus of the center id part of a circle ie an arc .... the angle subtended by thus ar at the origin is @
find cos@
-
UP 0 DOWN 0 0 9

9 Answers
(2) let (h,k) be the centre
since the coordinate axis is touching the ellipse, origin is the point from which the two tangents are drawn.
now write general eq. (x-h)2/a2 +(y-k)2/b2=1
and then use T=0
sow homogenise T=0 with ellipse and put (coefficient of x2)+(coefficient of y2)=0
u will get the locus of centre
i have got also one elegant method for (2)
hint: since the tangents are perpendicular therefore the locus of point of their intersection is the director circle of ellipse .
but dude .... (x-h)2/a2 +(y-k)2/b2=1 is the equation og an ellipse whose center is at h.k but whose major axis is parallel to the co-ordinate axis ...... but this is not the case here na
we get only an arc of a circle while tracing the locus of the centre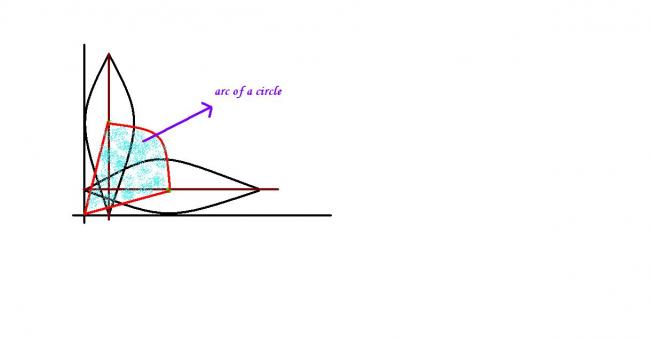
organic that is given in the question only that it forms an ark!!. ......