the sides of a triangle touch a circle x2 + y2 = a2 and 2 of the vertices are on the line |y|=b. find the locus of the third side............
-
UP 0 DOWN 0 0 1

1 Answers
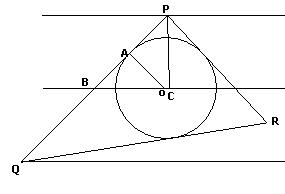
take a triangle PQR such that PQ , QR and RP be the tangents to the circle x2 + y2 = a2
P on line y = b and Q on line y= -b
draw perpendicular from center of circle to tangent PQ name it A now OA = a
angle AOB is α
co-ordinate of point of intersection of PQ and x-axis be B(aSecα,0)
draw perpendicular from P to x-axis name it C now CP = b
therefore angleBPC = α
hence co-ordinates of P will be P(asecα+ btanα,b)
similarly co-ordinates of Q will be Q(asecα - btanα,-b)
take co-ordinates of R(h,k) whose locus is to be found out
now using equation of tangents and condition of tangency can be found