nahi mani... question's perfectly rite... try karo...
Prove that from a point (a,b) of the circle x(x-a) + y(y-b) = 0, two chords, each bisected by the axis of x (rather x-axis), can be drawn if a2>8b2
[This is not my doubt, so provide complete solution for everyone's benefit ]
cheers...!!!
-
UP 0 DOWN 0 2 12

12 Answers
sir question ki language ko ek baar check karna
i wonder some wrong info is given................
Prove that from a point (a,b) of the circle x(x-a) + y(y-b) = 0, two chords, each bisected by the axis of x (rather x-axis), can be drawn if a2>8b2
BOLDED KA KYA MATLAB HAI???
thr's sum fishy in this q ....................past year iit q hai:P
method goes like this
let it pass thru (h,0) ..........this is d pt wich bisects d chord
so itz equation is
T1=S1
nw it also passes thru (a,b) .accordin 2 ur q
so satisfy dt condition
then u get a qudratic in h
solve for b^2>4ac
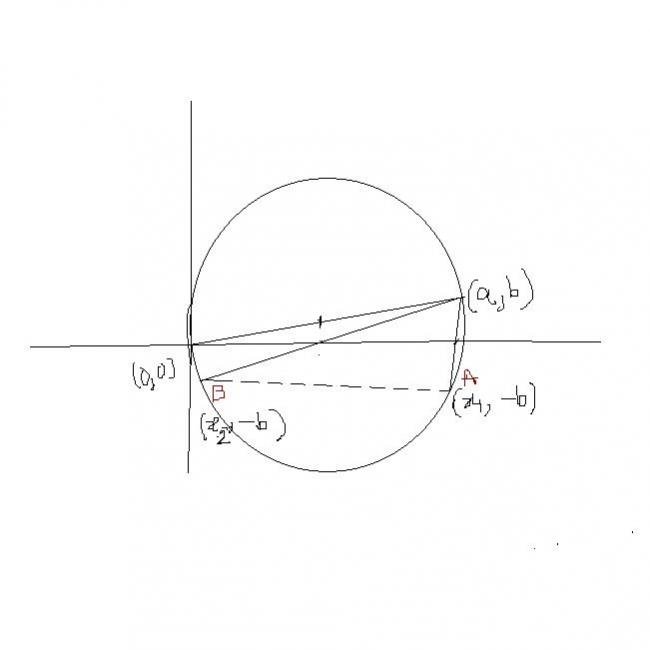
Given circle --> x2 + y 2 = ax + by
Let the mid-point of the chord be (p,0)
Equation of chord having mid-point (p,0) is
T = S1
px - a/2(x+p) - b/2y = p2 - ap
2p2 - ap - 2px + ax + by = 0
(a,b) is a point on this chord
2p2 - 3ap + a2 + b2 = 0
This is a quadratic in p.
Since, there are two values of p (2 chords are drawn)
Discriminant > 0
9a2 - 8(a2 + b2) > 0
a2 >8 b2.
Please tell me if I'm wrong.
ALL THE BEST
I agree with ragadeepika. :)
Another method :
Let P(a,b) be the given point, even O(0.0) lies on the given circle. Also observe that O,P form the ends of a diameter, so the centre of given circle will be C(a/2,b/2).
Now, the circle with C,P as ends of diameter should intersect X-axis twice so that two chords can be drawn from P which get bisected by axis of x. (observe this carefully, if needed i'll post explanation)
equation of circle with C,P as ends of diameter is : (x-a)(x-a/2)+(y-b)(u-b/2) = 0
substituting y=0 and applying the condition of discriminant > 0, we get a2>8b2
so x1,-b lies on the circle.
thus it shud satisfy the equation x2+y2=xa+yb
=> x12 + b2 = x1.a - b2
=> x12 - x1.a + 2b2 =0
sice x1 should be real... therfor, D> 0 [not equal ofcrs!]
so, a2 > 8b2 . proved :)
well, one guy asked me for explanation to my previous post. so this is for him.
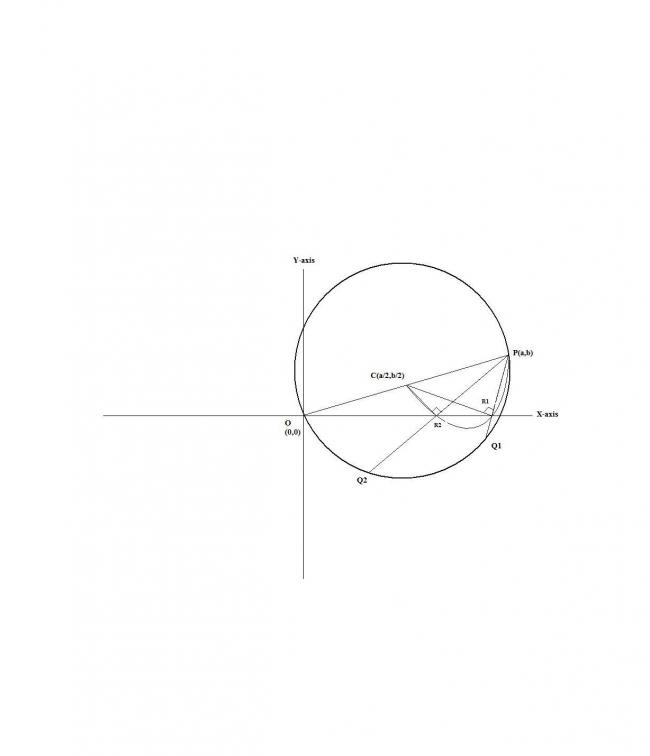
Explanation :
1) The perpendicular from centre of a circle to its chord bisects the chord. [observe with reference to CR2(perpendicular to)PQ2 and CR1(perpendicular to)PQ1]
2) Angle formed by a diameter of a circle in the semi-circle is 90o [observe with reference to angle(CR2P) and angle(CR1P)]
hope this clears ur doubt :)
correct me if i am wrong !