equation

the center is at the perpendicular bisector of the line joingin (1,1) and (2,2)

so its center is on the line ?? x+y=3??

then on this line draw a circle!!

Now think of the graph or solve it by taking a point (h,3-h)

and the distance from the x and y axis have to be less than the radius..

This is best solved by using a graph! (you will get the limiting case directly :)

This cant be an excuse eureka....

You have to improve deficiencies..

This makes the quesiton very simple!

But theoretically u have to take the thing that the distance of the point from 1,1= distance from 2,2 = min(x , y ) coordinates of the center of the circle

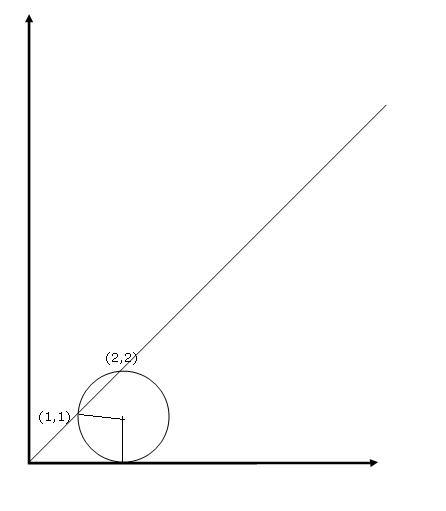
the center, as we discussed is on x+y=3

let it be (h,3-h)

for the limiting case,
distance from (1,1)= distance from x axis or y axis which ever is lower!

thus, (h-1)²+ (3-h-1)² = (3-h)²
(h-1)²+ (2-h)² = (3-h)²

2h² - 6h + 5 = 9 -6h + h²
h=2 and -2
h is in the first quadrant .. so h=2

center is (2, 1)

so the circle's equation (x-2)² + (y-1)² = 1

There will be one more equation eureka.. try to get it!!! by the same method!!

yes indeed satan :)