24dont calculate that much precisely..i ahve ans as
9√32(√3-1√3+1)
Q1 If point moves insdie equilateral triangle of side length 3 unit such taht it is nearer to the angle bisectors of the triangle than to any sides.then calculate area traced by point P
Q2 Let L1=y/b +z/c ;x=0
L2=x/a -z/c ;y=0 are two lines .Aslo 2d is shortest distance b/w lines L1 and L2.Then
a)plane containing L1 and parpallel to L2 is unique
b)eqn of plane containing L1 and parallel to L2 is given by x/1 -y/b -z/c +1=0
c)1/a2+1/b2 +1/c2 =1/d2
d)1/a2+1/b2 +1/c2 =d2
**plz dont post BT solns..i am looking for somethign diff
-
UP 0 DOWN 0 1 6
6 Answers
11)teh resultant region which i m getting is a regular hexagon of side length .634 so area getting as 1.044
1the green region is the required region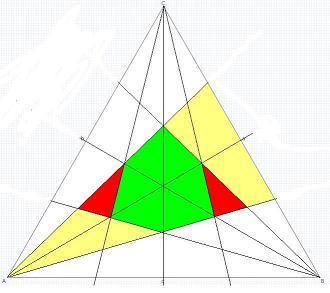
can u find the area?
may be i made a mistake in finding the area
its actually a regular hexagon....though may be not looking like a regular one in fig
4
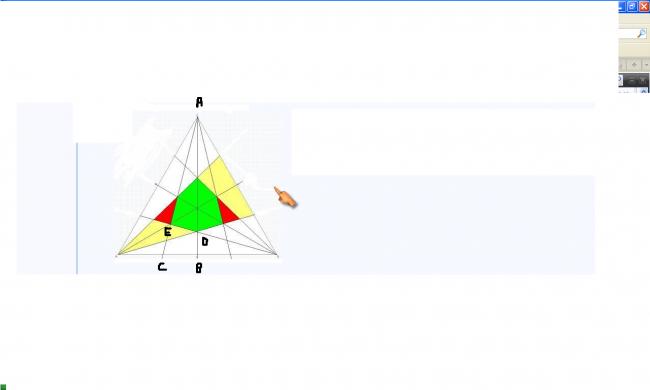
Using similarity of triangle ABC & ADE
(3/√3 + s )/ (3√3/2) = s/(3/4)
s = √3/(2√3 - 1)
Area of Hexagon = 6 x √3 / 4 x (s)2 = 9√3 /[ 2 (13 - 4√3) ]
4Ans is same or not?? The denominator is differing i guess
Where's the mistake??