let us not let this thread die away without being solved..........
evryone pls tryyyyyyyyyyyyyyyy...............
nishant sir..........pls solve
a good question for jee aspirants new to this forum......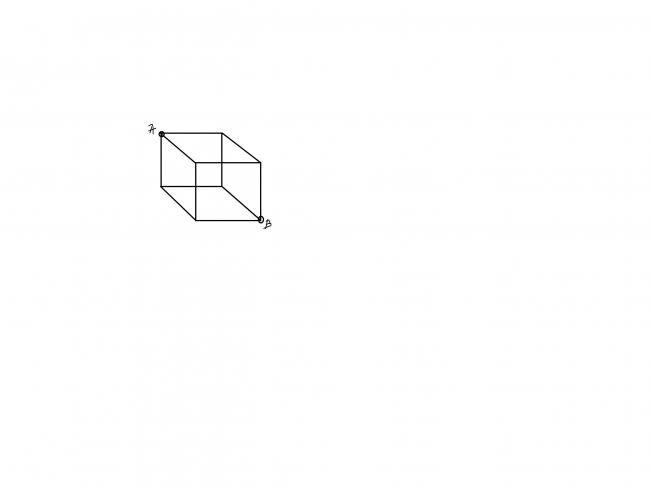
suppose an insect (without wings) has to crawl from vertex A to vertex B of the cube of side a shown in the figure
then find the minimum distance that the insect has to travel to reach from
vertex A to vertex B........
p.s. injun joe stay away
-
UP 0 DOWN 0 2 51

51 Answers
u cannot move inside uttara...warna nishant bro ye question sayad hi post karte..lol
EVERYONE KNWS THE SHORTEST DISTANCE BETWEEN TWO POINTS IS A ST LINE..so dat wouldnt be apossible answer to such a long thread
ANOTHER QUESTION PERTAINING TO THE TOPIC
shortest path around cylinder
An ant starts at a point on the bottom edge of a right circular cylinder of radius and height . If the ant makes complete circuits around the cylinder and finishes at a point at the top edge directly above its starting point, find, with justification, the length of its shortest possible path.
basically what mistake uttara is commitin is that she is moving the ant on straight line.....it wont move on stragiht line inside the cylinder..beczo of curvature..
R√2 is obtained when we take the path across a chord which makes 90° at d centre of d circle...
if i take a case of values,my answer is smaller dan uttara...plz check
@eureka123 : Do v need to consider the insect ???? In Nishant sir's Qs it's just mentioned to find the shortest dist b/w two opposite vertices on a cylinder !!!
@maths _psy : How R √2 I don't get u ? Which chord n circle r u considering?
well I read teh topic of thread and replied.....If it is not insect then not much to wory..but if it is insect then we certainly cant go that way[6]
everyone see this for hint
http://www.mathhelpforum.com/math-help/geometry/45778-shortest-path-around-cylinder.html
i hav posted the ans already scroll up...i jus wana confirm..and confirmed!!
@xyz : Y do v need to open up the cylinder when v have no conditions like not travelling
inside I dont get ur point!!
Let me give a hint..
what uttara and maths_phys have done in post 28 and 19 respecitvely are correct.. (Both take a straight line)
But there is one small missing thing....
The final answer will depend on the function/. relation between r and L
Think about it?
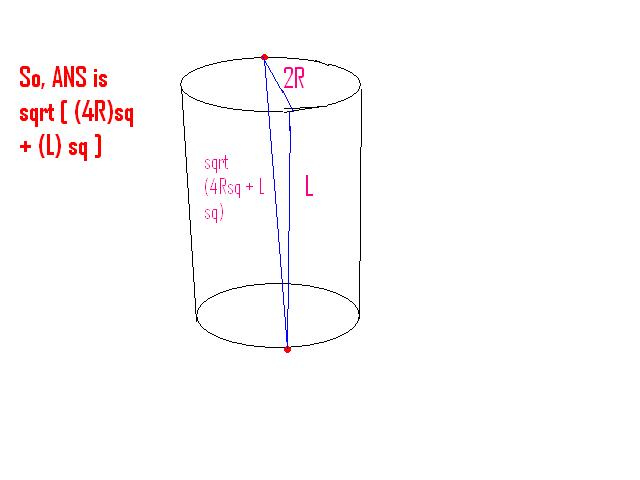
@Nishant Sir can we say the shortest distance is achieved at L = 4R ???????????/
i.e. shortest dist = √20R2
no uttara.. the way I think this will work.. is that
We have to compare 2R+L and √(piR)2+L2
which is 4R2+4RL+L2 > (piR)2+L2
which is 4R2+4RL > (piR)2
0 > (piR-4L)R
0 > (piR-4L) (since R>0 always)
so if R<4L/pi
then you will have the first path
otherwise the 2nd path... [1]
But Nishant Sir y do v need to compare 2R + L & √(piR)2 + L2
I've considered √(2R)2 + L2 < √(piR)2 + L2
Qwerty dont worry about pinked posts as much.. it is my request to all users here.. I kind of feel bad when i see that the motivation to interact here is the number of posts or number of pinked posts etc..
We are all here not to give or take more pinked posts but to learn new stuff.. Even I keep learning everyday here.. Believe it or not, I think that I am one person who has learnt most here!
i am unable to understand how we are getting to equation of conjugate hyperbola from the standard eqn of the hyperbola .please help.
i am unable to understand how we are getting to equation of conjugate hyperbola from the standard eqn of the hyperbola .please help.
i get the soln...:P
cut open the cylinder
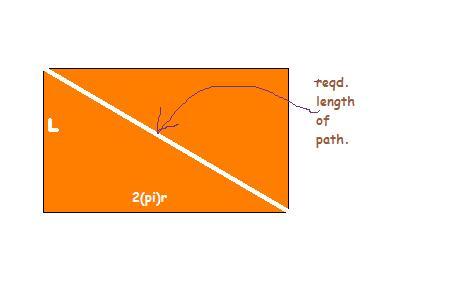
reqd distance is..\sqrt{(2\pi r)^2+L^2}
thats the answer....for sure...[1][1][1]
@ ATGS : thats precisely what everyone else was discusing ,,,yaar :D
there will be cases...
It seems so.
Or am not thinking deeply enough.Latter seems more likely
i didnt intend u to answer sir,,,,,,,,,pls let some junior answer this one
A slightly different and seemingly difficult... . but it will be a better question....
what will be the shortest point on the opposite "vertices" of a cylinder
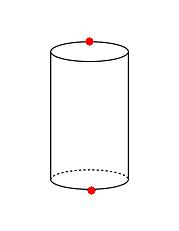
Do I come in juniors?? I've seen this one before (though not nishant sir's)