injun read the p.s.
a good question for jee aspirants new to this forum......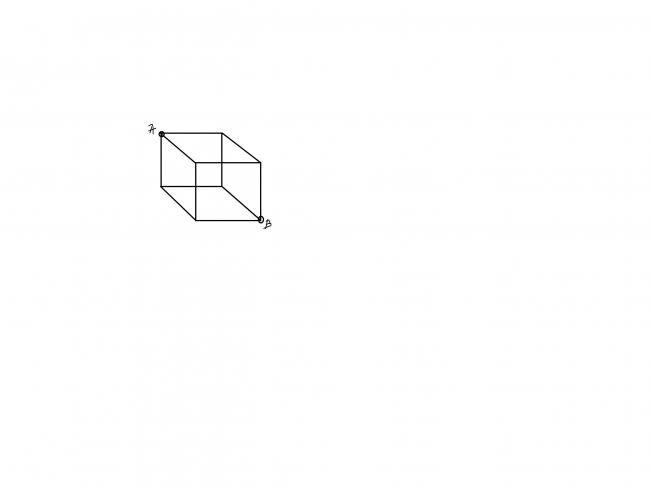
suppose an insect (without wings) has to crawl from vertex A to vertex B of the cube of side a shown in the figure
then find the minimum distance that the insect has to travel to reach from
vertex A to vertex B........
p.s. injun joe stay away
-
UP 0 DOWN 0 2 51

51 Answers
The question I gave just not is one that even I had not seen before :D :D
But i think there is a good solution too ;)
Sir's question
Shortest distance is 4R+L
R- Radius
L- Length of the cylinder
first move towards the top.. Length L
then cross the diameter.. 2R
hence the answer :)
"Removed my answer"
funnily this question also i discussed in the class IX that i am taking :D
Unless I am sleeping.. this one is a sitting sitter
\sqrt{(\pi R)^{2}+L^{2}}
incomplete !
i did arshad's ques in class 9....but i got trapped in it at dat time
in my above diagram....d shortest distance will be by moving from A to B ,den to C....where B and Cmake 90° at the centre of the bottom circle...so the minimum distance cumes out as
√[ (Ï€R/2)2 + L2 ] + R√2
for such questions .....convert d 3D fig into a 2D fig ....then its a pythagoras type question [ thats how i solved the cube wala]
btw is the answer of the cube one = x(√5)???
[ shortest length = √(2x)2 + x2 ]
There is much moer to this question...
i mean the cyllinder one...
[1]
sir,i did it by pythagoras theorem in a 2-d figure....sir.,plz give d solution....
@Nishant Sir : Can this be a solution?
First travel R to reach the centre of top circular edge and then travel √ R2 + l2 to reach the required point on the opposite side of the bottom circular edge
Shortest since R + l > √R2 + L2
Therefore total dist = R + √R2 + L2
