ABC is a right angeled isoceles triangle with B=90° .it slides in the X-Y plane with its vertex A on the Y axis and with the vertex C on the X axis and such that the origin and the vertex are at the opposite side of AC.find the locus of B
-
UP 0 DOWN 0 0 25

25 Answers
yes varun.. exactly!
then where is the confustion!
it will be these 4 segments of some length (depending on the length of the hypotenuse... )starting at some point (depending on the length of the hypotenuse) and ending point(again depending on the hypotenuse!)
Now we have not taken a fixed length. It is just a
and it is definitely not the lines x=y and x=-y
more over origin is not a point even in the union of all possible cases of the hypotenuse!
yes, it is a circle , but you can't say what is the radius right ?
Then for this question, the answer is some part of the line x=y but you can't specify which part it exactly is ..
well varun.. ur argument only strengthens the argument of sky!
But lets not get into this discussion... I think we all understand and get the point. Period :)
But I think varun you should try to do what sky has done if it comes in the exam. I am not at all convinced by ur argument!
I understand clearly what u are trying to say. But I think I can say will certainty that u are not right..
I will give an example: What is the locus of the points which are equidistant from a fixed poitn? (Is it a cricle or does it become the whole plane.. just because the radius or the distance is not given?)
@sky, well then they said "and the vertex are at the opposite side of AC"
So B must be opposite of the origin wrt to AC .. now in what you showed you showed, some won't satisfy that :S
And of course, any ABC if a triangle will be only a triangle... can't be more than 1 :(
And they didn't give what is 'a' in the triangle and how can you use that in the solution ? or at least it must be eliminated...
I understand what you are doing but you can't just use some 'a' right ? This is the general case i think not for a constant BC
Sky: din solve it though... rather cudn solve it.... all dirty things wre coming .. so left :(
@ Well sky if thats the case try with
A rt triangle in same situation but not an isosceles one but having sides as a and b :)
i.e AB=a
CB=b
angle(b)=900
Locus of B....
yes hypotenuse is formed but they didn't say that it must be a constant right ?
well varun
When they say that the triangle is fixed.. the hypotenuse is as well..
Sky's answer to me is correct :)
They didn't say that the lengths of BA and BC are constant right ? The only condition is that they must be equal and on the axes and B should be on the other side...
So if the lengths of BA and BC are decreased and increased, the locus of B is every point on the x=y line except the origin where it doesn't form a triangle...
hmm.. this is a good one..
A=(0,t)
C=(√a2-t2, 0)
Now let B= (h,k)
so what we can get is that ....
C is at a lenth a/2 from the center of the chord AC. and perpendicular to it.
Does this help??
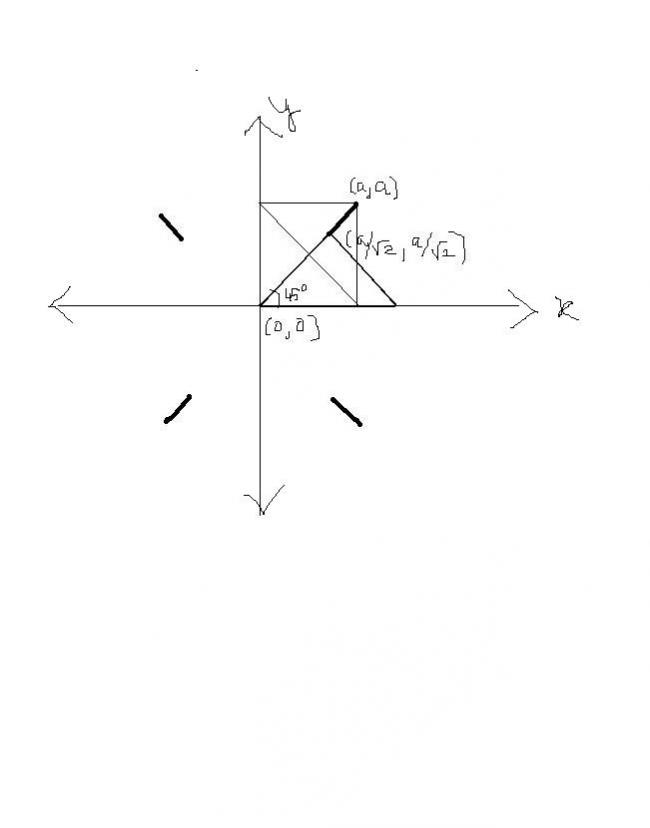
its x=y between (a,a) and (a/√2,a/√2)... in all the four quadrants...
din solve it though... rather cudn solve it.... all dirty things wre coming .. so left :(
wat i did,,, actually cut an isoceles right triangle (corner of a page).. and tried to move it along two perpendicular lines...
If the slider can change its axes, then it will be these segments in all the 4 quadrants!!!
But I guess i will try and solve on paper tommorow...
really really drowsy now...
gnite :)
no varun
i think (without solving!)
it would be a line segment between (a,a) and (a√2,a√2)
where a is the length of the base and height AB=AC=a
just use geometry
see one point will be given when the line AC tends to x axis, or y axis..
the other by symmetry when x=y ie when the both coordiantes of A and C have equal length on the respective coordinates.
It definitely cant be the whole x=y line!!
That is what i meant
Even if it comes out to be that.. u have to see whether it is really the whole line or is it the line segment!
no i dont think that will be the case! to be true i havent tried it with a pen!!
just able to get that the B lies on the line y=x !!
..... now, its not like that locus of B is the whole line y-x==0 !!