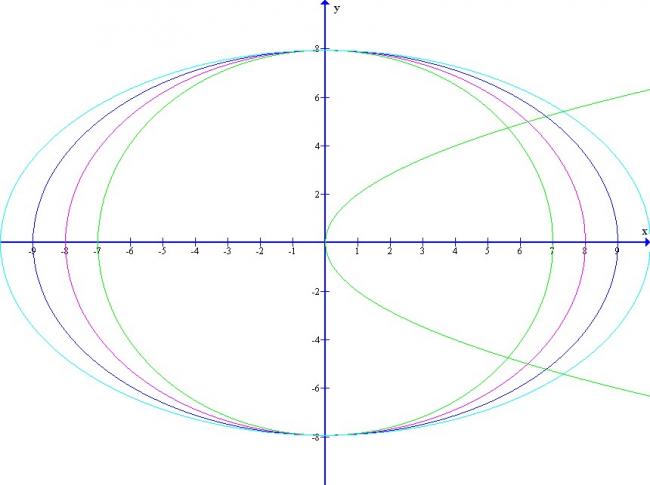
Given are two curves x2/a2 +y2/63 =1 and y2=4x
The maximum integral value of a for which there is only one common normal to the two curves is:
A. 7
B. 8
C. 9
D. 10
pls help!!
-
UP 0 DOWN 0 0 9

9 Answers
@AMIT
TERE KO IIT KI KASAM
AAGE SE GRAPH PLOTTER USE BAND KAR DE
IF U WANNA IMPROVE UR BASICS
yaar
i am almost done with it
i am getting
a2=-63x/2
but the fact that both the curves have a common normal is hard to digest[257]
x2/a2 +y2/b2 =1
equation of a normal is given by
ax/cos θ - by /sin θ = a2 - b2
y=a/b tan θ x - (a2/b - b) sin θ
y=mx-2m+m3
m=a/b tan θ
m3 = - (a2/b - b) sin θ
(a/b tan θ)3 = - (a2/b - b) sin θ
god only knows what i have done and where i have reached :(
sir jee
maine application of derivative se kiya tha
normal ki slope nikali
aur equate kiya
usse jo condition aayi that has been mentioned in #6
usse aage kuch banta hai to bana do
but please give the reply to the query in #6
eqn of normal of an ellipse in terms of slope( something i dint remember)
y=mx+(or)-m(a2-b2)/√a2+b2
eqn of normal for parabola
y=mx-2m-2m3
getting something very tough to solve
but i think the method is fine
equation of norml 2 ellipse aapko pata hoga
nw dat pases thru d focus of d parabola ..... :)