BC is latus rectum of a parabola y2=4ax and A is its vertex , then minimum length of projection of BC on a tangent drawn in the portion BAC is
-
UP 0 DOWN 0 0 3
3 Answers
1projection will be BC cos θ where theta is given by
tan inverse(2a/y) = tan inverse(1/t)
= sin inverse(1/√1+t2)
for latus rectum t = 1
so angle is 45 degree
so the minimum projection is 2√2a
1
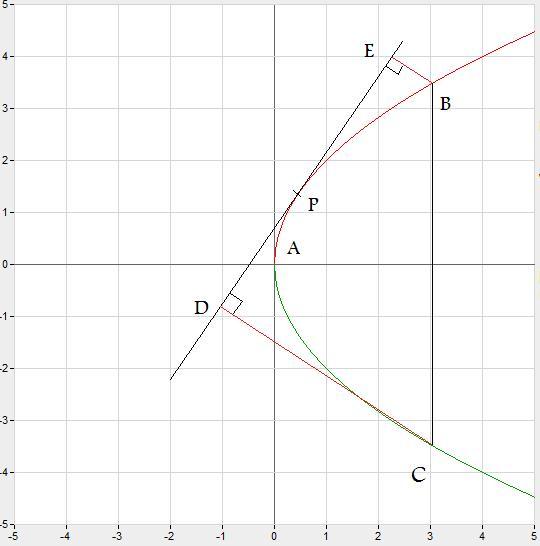
In the figure, DE is the projection of BC on a tangent drawn at point P.
As you can see, as point P moves along segment BAC, the length DE increases and becomes maximum when P is at origin (and DE=4a) and it again it reduces.
So, the minimum of DE will be when P is at B or C.