sorry edited
1)LET C1 and C2be two parabola x2=y-1 and y2=x-1.let p be any point on c1 and Q be any pont on C2. P' and Q' are the reflection of P and Q respectively w.r.t y=x line
then proove:
!)Prove PQ>min(PP',QQ')
2)hence determine P0 and Q0 point on c1 & C2 respectively such that P0Q0<=PQ for all position of P and Q respectively on C1 and C2 curve.
2)prove that on the axis of parabola y2=4ax there exist a point P,which has property that if a chord AB of parabola be drawn through P then (1/AP2)+(1/BP2) is a constant for all position of A,B on parabola.hence determine the co-ordinate of point P and the constant value.
-
UP 0 DOWN 0 0 4

4 Answers
i think that the last question should be 1 /AP2 + 1 / BP2 , because then the point would be (a , 0) and the constant would be 1 / a.
Q1 is really good ques
P=(t,t^2 +1)
Q=(s^2 +1,s)
P'=(t^2 +!,t)
Q'=(s,s^2 +1)
Clearly PP'QQ' becomes isoceles trapezium (becoz PQ' ll P'Q and PP' ll QQ' and (PQ')^2=(P'Q)^2 )
now to prove PQ >= min {PP',QQ'}
Let min {PP',QQ'}=PP'
=> PQ2≥PP'2
......
=> f(t)=2(t2-t+1)2
Minimising f(t) we get t=1/2
=> P=(1/2 ,5/4) ,P'=(5/4,1/2)
also PoQo≤PQ for all pairs (P,Q) where P lies on C1 and Q on C2
alternatively
both the equation are symmetry about y=x......as it is inverse of each other..
now the minimum distance between 2 curve will be the line normal to both the curve.......so at point P0,Q0.....tangent would be parallel.....wich would be parallel to y=x
the slope of tangent at P0=the slope of tangent at Q0=slope of (y=x) =1
now diffretiate y=x2+1
dy/dx=2x=1
so x=1/2......since this point lie on parabola x2=y-1.....y=5/4
p0=(1/2,5/4)......q0(5/4,1/2)
see diagram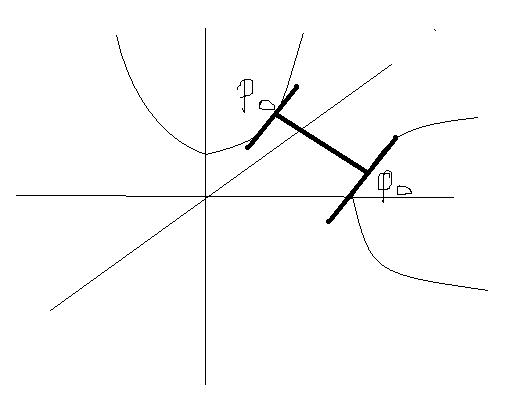
though the tangent at p0 and q0 and y=x are not lukin parralel in my digram......but actually they are