23the curve given will be the upper semicircle of x2 + y2 = 1 [ i.e part of circle above x axis ] ...but i m not able to interpret wat is max { |x| , |y| } ≤ 4
please explain what does max { |x| , |y| } ≤ 4 . stand for in the foll ques?????
Cosnider the region R which is enclosed by the curve y ≥ √ 1 - x2 and max { |x| , |y| } ≤ 4 .
The slope of a family of lines defined as m(t) = - sin2t + sint + 1,
where (t , 2t + 0.4) lies inside the region R
[Q 1 ] the area of region R is
[a]8 + \pi /2 8 - \pi /2 [c] 4 + \pi /2 [d] none of these
[Q2] All possible values of t are
(a) [ 0.14, 1] (b) [ 0.14, 0.5] (C) [0.28, 0.5] (d) [ 0.28, 1]
-
UP 0 DOWN 0 2 11
11 Answers
23
3
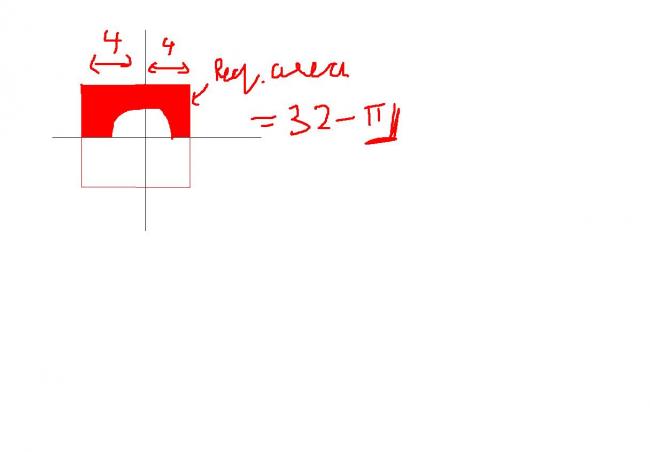
its simple qwerty its just a square of side 8!!!!!!!!!!.. think abt it ..
23ohkk..tnx ..
so it means that max value of |x| and |y| is 4 right ?? ....
and wat abt the second one .....
3its simple t,2t+0.4 ... shud satisfy the 2 inequalities ........ i think the m thingi is a time waste ...
23actually there was a simple question on m(t) ..... i didnt post it ..
23@ iitimcomin sorry but ur answer isnt matching with the solution given ...........it is given as follows ....
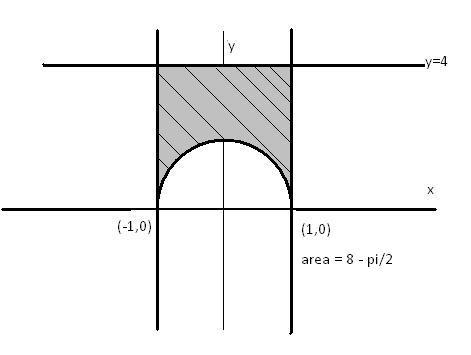
this is the solution given ..i m not convinced much ...is it correct guyz??
62Yes it is because for x>1 the region is outside the domain of the function...
(I overlooked that )
23and sir max { |x| , |y| } ≤ 4 means a square of side eight with centre at origin right ??