The vertices of a triangle ABC lies on a rectangular hyperbola such that the orthocentre of the triangle is (3,2) and the asymptotes of the rectangular hyperbola are parallel to the coordinate axis. if the two perpendicular tangents of the hyperbola intersect at the point (1,1).
i> The equation of the asymptotes is
(A) xy - 1 = x - y
(B) xy + 1 = x + y
(C) 2xy = x + y
(D) none of these
ii> Equation of the rectangular hyperbola is
(A) xy = 3x + y - 2
(B) 2xy = x + 2y + 5
(C) xy = x + y + 1
(D) none of these
262Ans : i)b ii)c
i)meeting point of perpendicular tangents → director circle.
radius of director circle for rect. hyp. = √(a2-a2) = 0
thus the point is the center of the hyperbola
ii) use the property that the orthocenter of the triangle ABC will also lie on the same hyperbola.
36@Aditya - ya ok... but if the radius of director circle is 0 then will the point of intersection of perpendicular tangents be the center...!!
36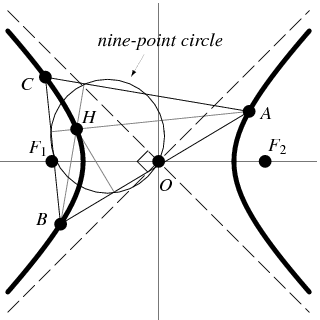
the orthocentre of the triangle inscribed in a rectangular hyperbola lies on the hyperbola itself... can be seen from the above figure...
and suppose if it is drawn in some other fashion like
only in one if the branch (not involving the other) then also does the fact hold good?
71Fiitjee wale bhi book se copy karne lage questions..
f the radius of director circle is 0 then will the point of intersection of perpendicular tangents be the center...!!
Yes it is.