roots

one can also use Rolle's theorem. If there is, apart from x=1, any other root, say α, then consider f(x)=ex-1+x-2 in the interval [1, α]. We see that in this interval f(x) is continuous and in the interval (1, α) f(x) is differentiable. Further, f(1)=f(α)=0. Hence, by Rolle's theorem, there should exist at least one point c in the interval (1, α) where f'(c)=0. But that's a contradiction since f'(x)>0.

I never heard of Rolle's Theoreme yet so you can simply do it by drawing the graphs..

e^x-1 + x - 2 = 0
or, e^x-1 = 2 - x

Sketch the graphs of f(x) = e^x-1 and f(x)=2-x...

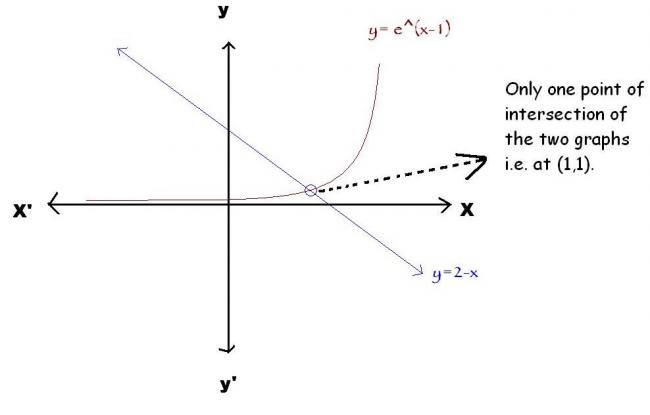
Hence only one real root of the given equation...