1I m not getting how to do it..Please reply..
If the tangent from a point P to the circle x^2+y^2=1 is perpendicular to the tangent from P to the circle X^2+y^2=3.Then find the locus of P..
-
UP 0 DOWN 0 0 8
8 Answers
106locus of P is x2+y2 = 4
this can easily obtained by observing the nature of the two circles graphically
11Let (h,k) be the point of the locus at some instant.
We have
k=mh\pm \sqrt{1+m^2}
&
k=Mh\pm \sqrt{3+3M^2}
Use the fact mM=-1, and get the desired locus....now try!
19yes, i think i will proceed in the same way as soumik has done...that solves the sum nicely!
1No yaar it doesnt help...When we square to get m things complicate a lot..
106See both the circles are centred at (0,0)
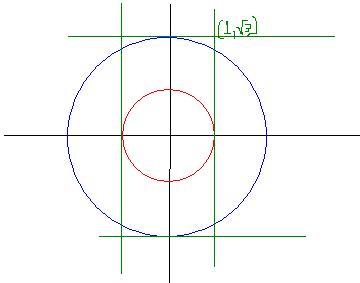
If you rotate that rectangle ... u will get the locus of P
obviously this is a circle.. which dist. from the centre is 2
So the locus equation is
x2+y2=4
This is for concentric circles only.
For any other system ,, u have to do what soumik has said