21
STRAIGHT LINES
1 ) Find the area of the triangle formed by the straight lines whose equations are x+2y-5=0; 2x+y-7=0 and x-y+1=0 withought determining the coordinates of the vertices of the triangle.
Also compute the tangent of the interior angles of the triangle and hence comment upon the nature of
triangle.
2 ) Find the equations of the sides of a triangle having (4,-1) as a vertex, if the lines x-1=0 and x-y-1=0
are the equations of two internal bisectors of its angles.
-
UP 0 DOWN 0 0 19
19 Answers
21for third one see this..........
okh ,,,,i m unable to post the diagram,,,,,so here i m explaining mah solution,,,,,,let OAB be the triangle.....where OB be the line y=m2x and OA be the line y=m1x........
H be the orthocentre ,,,i.e. intersection point of two altitudes OD to AB and AE to OB.........
m1 and m2 are the roots of equation b@^2+2h@+a=0
so m1+m2=-2h/b
and m1m2=a/b
slope of OD=-b/a so the slope of AB = -a/b
,,,,now equation of AB will be y=-a/bx+c'..............(b)
..where c' is the constant which we have to find,,,,,
now slope of AE=-1/m2........(coz m2= slope of OB and AE is perpendicular to OB)
so equation of AE is y-b=-1/m2(x-a)...............(a)
this line will intersect y=m1x....so put y=m1x in this line
we get m1x-b=-1/m2(x-a)
from here we get the x=(a+bm2)/(m1m2+1)..................................(1)
from y =m1x...we will get y=(m1m2b+am1)/(1+m1m2)...................................(2)
now put this y and x in equation (a) above u will get c'=(ab-2ha+a^2)/(a+b)
now from (b) and all others equation u will get answer as.....
(a+b)(ax+by)=ab(a+b-2h).............
http://www.goiit.com/posts/list/analytical-geometry-hey-guys-and-gals-try-this-a-triangle-has-970427.htm
62For question 6, the best way will be to use pure geometry...
If you cant think then post me a message I will post the complete solution...
21hey man dont ask me its derivation.......i dont hav it....i jus know the formula....if u want to know.....better asks nishant sir or prophet sir or kaymant sir.....they will be able to tell u nicely....
1the equations u used to get the area!!whts the inspiration behind that!!i mean can u explain to u got that formula???
post 5
1let third coordinate be (x1,x2)
then find the orthocentre usuing the three vertices n equate....
using two vetex get the slope suppose m ....then the st line through the third vertex is (x-x1)m=y-y1
fnd two such lines n find their intersection n equate it with the given orthocentre .....sums done!!
@deepak..plz answer the question i have posted above
1deepak i didnt get ur formula!!can u plz explain!!for the area question!!
1tangents of the interior angles can be found using....
tanθ= m1-m2/1+m1m2
42 more Qs
3 ). Atraingle has two sides y=m1x and y=m2x where m1 and m2 are the roots of the equation bα2+2hα+a=0. If (a,b) be the orthocentre of the triangle, then find the euation of the third side in terms of a,b and h.
4 )Two vertices of a Δle are (4 , -3) & ( -2, 5 ) and its orthocentre is (1,2) , find the coords
of the third vertex?
1This is not a triangle
they are 3 concurrent line so it was expected that area is 0
21for 1st question......well if eq of sides of triangle are
a1 x + b1 y +c1=0
a2 x + b2 y +c2=0
a3 x + b3 y +c3=0
then firstly find .....delta=determinant (a1 b1 c1)
(a2 b2 c2)
(a3 b3 c3)
then area of triangle is
(delta^2)/(2mod(C1C2C3))
where C1 C2 C3 are cofactors of of c1 c2 c3.....in the determinant delta
now do it accordingly.....
4I guess this method is too lengthy
Anyone with a shorter rather simpler method????????
11Right now, I'm not getting any elegant method for the 2nd one.....
U see the other 2 vertices are (1,h) and (k,k+1).....Now use the fact that those lines bisect the angle between them to figure out the 2 variables h & k.
4St lines contd
5 ) Atraingle has two sides y=m1x and y=m2x where m1 and m2 are the roots of the equation bα2+2hα+a=0. If (a,b) be the orthocentre of the triangle, then find the euation of the third side in terms of a,b and h.
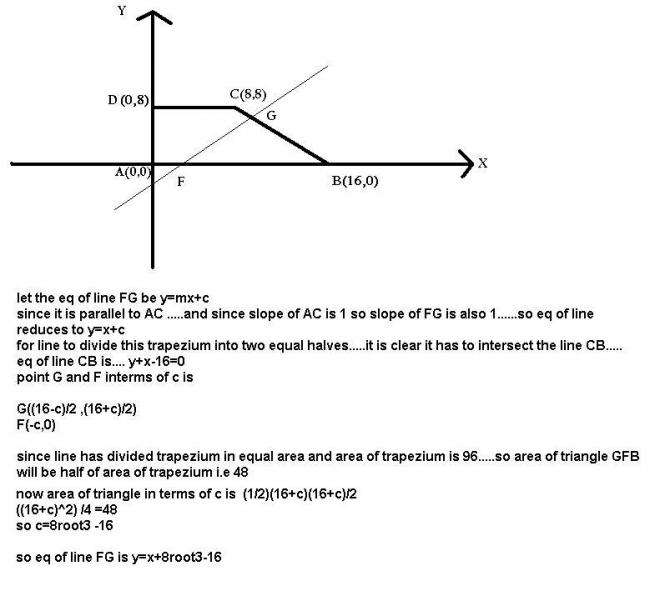
6 ) The coordinates of the vertices of a quadrilateral are A(0,0); B(16,0),C(8,8),D(0,8). Find the equation of the line parallel to AC that halves the area of the quadrilateral in the form of y=mx+c.