find the centre and the radius of the smaller of the two circles that touch the parabola 75y2=64(5x-3) at (6/5,8/5) and the x-axis
plzzzz explain
1ans radius =1
centre= 2,1
first of all differentiate and get dy/dy=32/(15y)
slope of normal=-1/(dy/dx)=-15y/32
but y=8/5
hence m=-3/4
further let radius =r
draw the diagram you will get
r+rsinθ=8/5
but sinθ=3/5
so r=1
further the equation of normal=
(y-8/5)/(x-6/5)=-3/4
we know at centre y=1 thus we get x=2
thus the answers
1
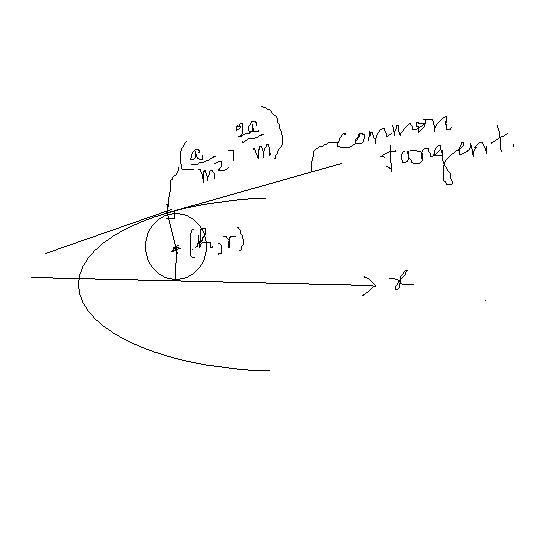
tangent to parabola:
y = m(x-3/5) + 16/15m ------------#1
tangent to sircle:
y-r = (x-h) + r√1+m2 ---------------#2
these are eqns of same tangent.. so equate their y-intercepts.
distance of center of circle (h,r) from (a/m2,2a/m) is r
--------------------------------#3
three unknowns - h,r,m .
can be solved.
11Parabola is y2 = 4.(16/15).(x - (3/5)) ≡ P
Let circle be (x-a)2 + (y-b)2 = b2 ≡ C
(6/5,8/5) satisfies C . So, (6-5a)2 + (8-5b)2 = (5b)2
or 100 + 25a2 - 60a - 80b = 0 ..............(1)
Equating (dy/dx)at (6/5,8/5) ,
4/3 = - (6-5a)/(8-5b)
or 3a + 4b = 10 ...............(2)
From (1) and (2)
C1 ≡ (2,1)
R1 = 1
C2 ≡ (-2,4)
R2 = 4