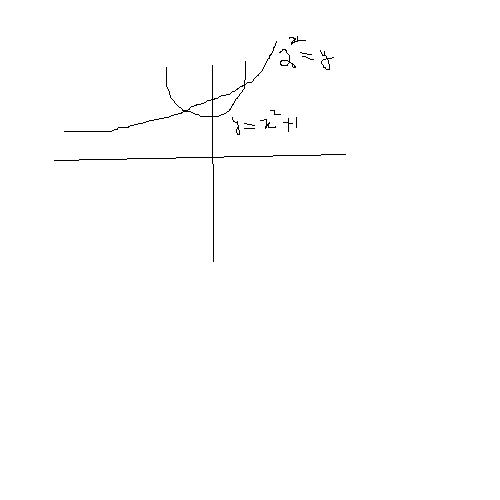
1can u please explain with the help of the graph , how there are 3 solutions of 2x =x2+1.
16 Answers
1
3let f(x)=2x-(1+x2)
clearly f(x)=0 at x=0,1
we want to chek out whether there are some other roots
for f(2)<0 f(3)<0,f(4)<0 and f(5)>0
so there is a root in between (4,5)
49let us see like this....i dnt kno if i can continue correctly till the end....but lemme try...
\frac{\partial }{\partial x}(2^x)=2^x.ln2\simeq 6.9(2^x)
\frac{\partial }{\partial x}(x^2+1)=2x
2x ≤ 6.9(2x)
equality holds at, 2x=6.9(2x)
solving this we get a value of x...
can any one solve this out???
after finding x, we find the value of 2x and x2+1
49no...the above approach leads to nowhere...at least i got lost....
simply we can see that the two functions become equal at x=0 and x=1...
and there is a root b/w 4 and 5....so there are 3 roots.....
49can someone help me i am stuck up.....i am getting a weird graph for y=2x...
can someone draw the graph of y=2x for me...please...[1][1]
49then we re getting 2 solutions from the graph isnt it.?.?.?.?.?.
49oh no....yes got it!!![1][1]
the curves do meet at very distant place...they re indeed converging...
thnxx qwerty.....for ALL the help u gave...
49i'll post the graphical solution tomorrow....aaj bahut niind aa rahi hai...for some inexplicable reason...bye all...[1]
1compare graphs of diff. of functions,their sign interchanges thrice
at x=0 2x<2x log2
at x=1 2x>2x log2
at x>>1 , 2x<2x log2
1the ryt ans has to be 2
there are two solutions and not 3...........
1No subhambar......it is 3....
see the original graph using online grapher....
the 3rd point is around x=4.26