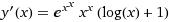I'M GETTING '2e'. But given 'e'. please help.
8 Answers
y = e^{x^{x}} => logy = xlog(e^{x}) => \frac{1}{y} \frac{dy}{dx} = log(e^{x}) + \frac{x}{e^{x}}.e^{x} = log(e^{x}) + x
=> \frac{dy}{dx} = e^{x^{x}}(log(e^{x}) + x)
At x = 1,
e^{1^{1}}(log(e^{1}) + 1) = e(1+1) = 2e
where log is the natural log, hence log(e) = 1.
Manmay is correct if my calculations are correct!
definitely the options didn't have 2e.
i got the ans as 2e but given was e so i had to leave it.
pritish bhaiya above should be wrong .
becuase when we use \log m^{n} = n\log m
you have to take out power on m. but you have taken the power on n. a mistake there
so . sloution would be like this
\ln y= x^{x}\ln e = x^{x
let\: z= x^{x}=> \ln z = x\ln x
=> z^{'}= x^{x}(\ln x+1)
=> y^{'}= y(z^{'})=y[x^{x}(\ln x+1)]
thus \: at \: x=1 \: y^{'}=e
oooo! I didn't notice..
yes then it's e..thanks for correcting me!
Ya Pritish u have made a mistake while taking out the powers...coz 233 is not equal to (23)3..so the final answer will be e...