23in (a) i m getting B= uoI2Ï€r(2r2 - a2)(4r2 - a2)
in (b) i m getting B= uoI2Ï€r(2r2 + a2)(4r2 + a2)
but i m not sure if it is correct
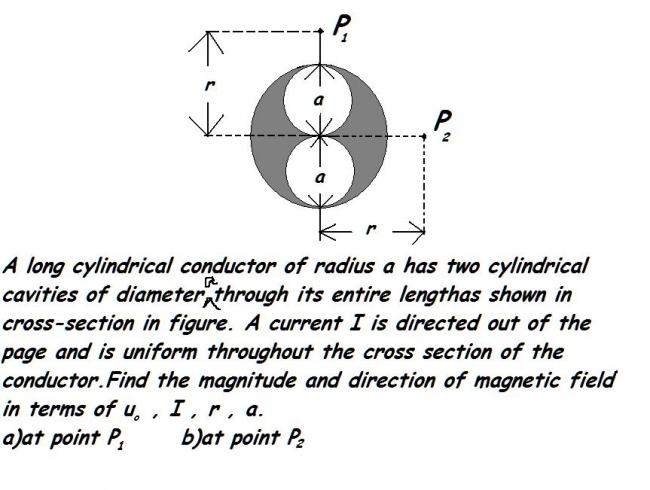
ans: a)uoI4r(2r2 - a24r2 - a2) to the left.
b)uoI(pi)r(2r2 + a24r2 + a2) towards the top of the page.
-
UP 0 DOWN 0 0 9
9 Answers
2323see first neglect the cavity and assume that that the cavity is absent , and find magnetic field B1
now assume that there was a cylinder in the cavities , find magnetic field B2
and B3 due to these cylinders, but since these cylinders are not there remove it frm B1
hence net magnetic field = B1 - (B2+B3)
but remember that current thru the small cylinders will be I/4
11bhaiya in (b) please tell how to find B2 and B3...
will the dist of P2 from the centers of of the two cylinders to be subtracted will be √(a2/4) + r2 each...????
23yes,
u will find |B2| =|B3|
B2+B3 = 2 |B2|r(r2+a24)1/2 (-j)
(i.e horizontal components cancel out and vertical components add up)
= 2μoI r4(2π)(r2+a24) ( - j)
(ignore silly mistakes)
11thanks bhaiya....i think that the answer might be wrong...neways thanks bhaiya for telling me the method how to slove it....!!!!
1@ Qwerty
I got the same answer given but with a slight change-
In denominator (in part a ) there 4(pi) and not 2(pi)
I will tell your mistake.
You assumed that the conductor extends infinitely on both sides of point P1 which is not true. Here the angles subtended by the ends of the conductor will be 0 and 90 (not 90 and 90) as the point P1 is directly above the end of the conductor.
23but it is given that it is a long cylinder and no where it is mentioned dat the pts are at one end of d conductor !
1Yes you are right, but from the figure P1 is directly above the cross-section... I know we can't tell anything exactly but since the answer I get my way matches with the book's answer, we should assume that the points P1 and P2 are at the end
the pi difference in a is just a printing mistake.
If you do it my way you get same answer in b