Capacitor C1 will discharge acc to the equation,
q = q0 e-(t/time const) ..........................(!)
where time constant = c1 R
Therefore, q=q0 e-(t/RC1)
Whereas discharging current is given by,
i = -(dq/dt) = (q0/C1R) e- (t/RC1) ...........................(2)
At the given instant i = i 0
From equation (2),
q o e-(t/RC1) = i 0 C1R at this instant
Charge C1 at this instant will be q = (i 0 C1 R)
Now this charge q will later on distribute in C1 and C 2.
Therefore, U i = q2/2C1
and U f = q2/2(C1+C2)
Therefore Heat generated in the resistance,
H = U i - U f
On substituting values, we get
H = [(I 0 R)2C1C2] / [2(C1+C2)]
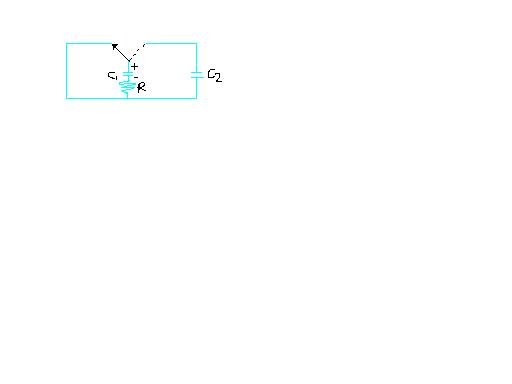
A charged capapcitor C1 is discharged through a resisitance R by Putting switch S in position 1 of circuit as shown in the figure. When discharge current reduces to I 0 , the switch is suddenly shifted to position2. Calculate the amount of heat liberated in resisitance R starting from this instant.
-
UP 0 DOWN 0 0 1

1 Answers
Tush Watts
·2009-08-16 01:26:39