how
V = Q1+Q2/c1+c2
please solve
pg 166
Q12). 2 conducting spheres radii R1 and R2 kept separated if spheres connected by conducting wire, find capacitance
Ans = 4*pi*epsilon not*(R1+R2)
Why is it parallel
Q47.b) capcitor 5 microfarad charged to 24V. another 6 microfarad charged to 12V. positive plate of first connected to negative plate of second and vice versa. find new charges on each.
-
UP 0 DOWN 0 0 9

9 Answers
We already know their individual capacitance..
c1=4Πεr1 c2=4Πεr2
Say they have initially charges Q°1 and Q°2. Thus Q°1 + Q°2 =Q°
say they hv potentials v1 >v2
After connecting them with a wire the charges start to flow from higher to lower potential until they attain same potentials.
V=Q1/c1=Q2/c2=Q1+Q2/c1+c2 ............(addendo)
V=Q°/c1+c2 (Charges are conserved)
Thus c1+c2 =Q°/V=Ceq
Thus Ceq=4Πε(r1+r2)
they will be in parallel......
47 b) 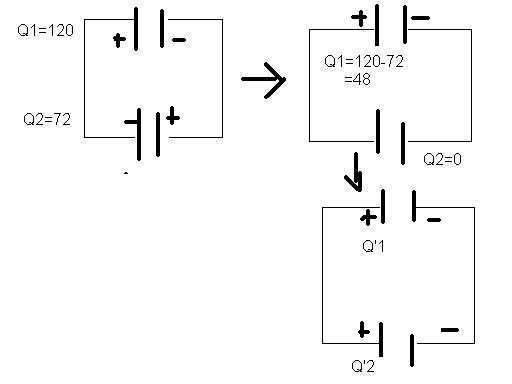
ie, Charge sharing takes place.........
now Q=Q'1+Q'2=48
Q'1=QC1/C1+C2=5*48/11=21.8μC
Q'2=QC2/C1+C2=6*48/11=26.2μC
That a mathematical property.........called addendo........
a/b=c/d=a+c/b+d..........
Q'1/C1=V=Q1/c1=Q2/c2=Q1+Q2/c1+c2 ............(addendo)
V=Q/c1+c2
thus Q'1=QC1/C1+C2....
Hey sandeep... its simple...
(1) since the spheres are connected by a conducting wire... the charged spheres are nw at the same potential.... hence at the same potential, equivalent capacitance is equal to the sum of the individual capacitances of the spheres.... i.e.
C EQ = C1 + C2
C EQ = 4πε0R1 + 4πε0R2
C EQ = 4πε0(R1 +R2 )
and Q2... is the correct apprach by Lanuk..... u can follow it....
u must remember that a single conductor can never form capacitance..
at least 2 conductors are reqd to form a capacitor...
in case of isolated sphere the second conductor is another spherical conductor of radius infinite and centre same as the entre of the conductor...
similar is the case for the second isolated conductor...
now the 2 conductors kept at infinity are always at same potential i.e. 0 thus they can be treated s if they are connected to each other by a wire
also we are connecting the 2 isolated spheres with a wire...
so by doing so we are making the 2 capacitances in parallel....and thus the net capacitance is C1+C2
for 47)b type of questions:
NEVER USE LAW OF CONSERVATION OF ENERGY!!
next:
use CONSERVATION OF CHARGE on each of the connected plate systems...
lastly..the new charges will be such that the 2 plates come to same potential
initially, Q1=C1V1
and, Q2=-C2V2
let final potential be V
so, (C1+C2)V=C1V1-C2V2
and from this u will get V
now u need to find C1V and C2V