21that does not helping at all, :D
please help
Please show me the charges appearing on each faces. A dilelectric is kept inside two conductor as shown in figure.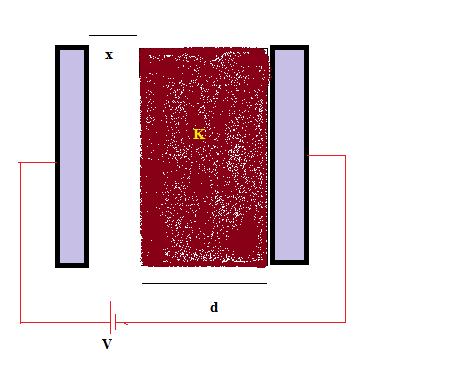
-
UP 0 DOWN 0 0 11
11 Answers
1this wil help
http://hermes.eee.nott.ac.uk/teaching/cal/h51emf/emf0017.html
21that's fine.
but here the dielectric is kept in contact with the conductor(on the right side)
49The charge on the outer surface of the plates is 0 ....
The charge on the inner surface of the plates is ±KAεod+Kx.V for the respective plates..
The charge on the either surfaces of the dielectric slab is ±(K-1)Aεod+Kx.V ...
I will give solution tomorrow..
But these are the right answers according to me..
@Ashish: Try to prove the results!
30
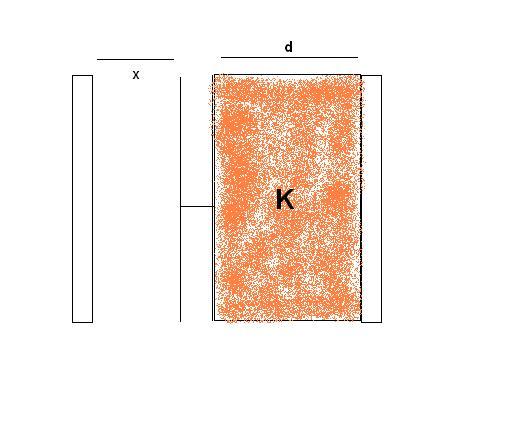
Thus if we calculate the equivalent capacitance for the series combination,
\frac{1}{C_{eq}}= \frac{x}{A\epsilon _{o}}+\frac{d}{AK\epsilon _{o}}
C_{eq}= \frac{AK\epsilon _{o}}{d+Kx}
Now, since in series combination, charge on both capacitors is same, we can say charge on first plate (connected to positive terminal of the battery) is
Q=\left( \frac{AK\epsilon _{o}}{d+Kx}\right)V
Similarly, charge on the capacitor with dielectric will be the same.
Now,
Q_{induced}=Q\left(1-\frac{1}{K} \right)
Therefore,
charge on the faces of the dielectric = \pm \left( \frac{A\epsilon _{o}}{d+Kx}\right)\left( K-1\right)V
But, I can't get why the charge on the outer faces of the capacitor plates becomes zero. [7]
49@Ashish: Answer to your doubt: Coz if the charges were not zero the field inside the conducting plates would not have become zero!