33u are asking for thin sheet?
we know that the electric field of an infinite thick sheet is
EF = surface charge density
epsilon
i have taken the gaussian surface as shown in the figure. It ends inside the thick sheet ( its embedded inside ). Alongside the thick sheet i have shown a planar lamina as well ( that's where my doubt lies!!!)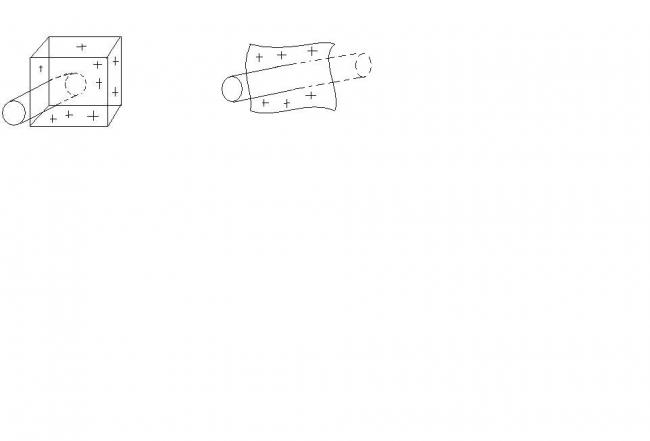
now,
in the lamina the gaussian surface passes through it. So its electric field should be
= 2 x surface charge density
epsilon
i.e. twice of the electric field calculated above..
BUT!!
we already know that the electric field of a planar lamina is
EF = surface charge density
2 epsilon
Now, my question is how is this possible????[7][7]
(i think something is wrong in the assumptions but i am not able to figure out the mistake!!!!).
Do think about it.....[12]
-
UP 0 DOWN 0 0 4
4 Answers
33I think u are telling for the thick plate....one end of the guassian suface is inside the sheet.
Then E.A=sigma.A/epsilon (as one end is inside we take only one side's surface charge density..)
we get the req result.
1abhishek please go through my question again.
i am not asking the formula for thick sheet.. I am asking the validity of the formula of a planar sheet.
Do reply if u are clear about this..
1look a thick sheet will be made from a huge no of thin laminas... isnt that true???
so, looking at the two gaussian surfaces we should take the electric field of a thin sheet ( think of taking out a thin sheet from that thick one and then looking at the gaussian surface ) to be twice of that calculated for the thick sheet...!!!
but actually its half of that!!!!!
do tell me if u are not clear about what my doubt is!!!