EASY - IIT 07

thank you sir... and sorry for dat stupid reply.

sorry I didn't see that already the derivation has been posted.

Use superposition. Assume that initially we had the entire sphere. Then, at any point within the sphere, the electric field is
\vec{E}_+=\dfrac{\rho}{3\epsilon_0}\,\vec{r}_+
(this result is obtained by using gauss law for a uniform sphere)
Here \vec{r}_+ is the position vector of the point with respect to the center of the original sphere.
Now, superimpose an equal but opposite charge density in the region where the cavity is required. This negative density will cancel out the positive density and we will get a cavity. Inside this (negative) sphere, the electric field at some point whose position vector w.r.t. its center is \vec{r}_- is
\vec{E}_-=-\dfrac{\rho}{3\epsilon_0}\,\vec{r}_-
So, now when we create the cavity, we add the two effects (vectorially) giving us the total field as
\vec{E}=\vec{E}_++\vec{E}_-=\dfrac{\rho}{3\epsilon_0}\,\vec{r}_+ - \dfrac{\rho}{3\epsilon_0}\,\vec{r}_-=\dfrac{\rho}{3\epsilon_0}(\vec{r}_+-\vec{r}_-)= \dfrac{\rho}{3\epsilon_0}\vec{\ell}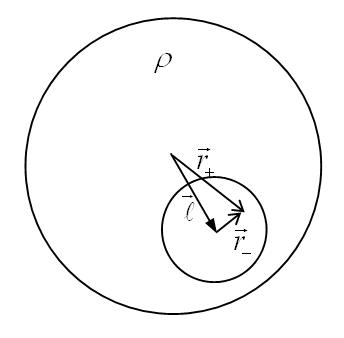

Wow!!!
'Nice one Eure!!

thnx yaar [1]

kayamant sir is rite

here is derivation for what sir said

sir, can u pl. tell how did u get the Expression for E in post #13

@skygirl: your reason in #6 is entirely wrong. The field is determined not only by the charges within the Gaussian region but ALL THE CHARGES PRESENT.
It may be worthwhile to note that the field within the cavity is
\vec{E}=\dfrac{\rho}{3\epsilon_0}\vec{\ell}
where \rho is the (uniform) density of charge and \vec{\ell} is the position vector of the cavity w.r.t. the center of the original sphere.
Needless to say that the field is non-zero and uniform.

poitn yaar!!

But,
I did by Va - Vb

then I got Va ≠Vb how cum [11] [7]

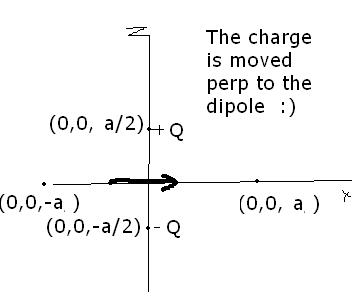
2) 0...........because the pt. charge is moved along the equitorial plane of the dipole

hmmm....... OK!!! k k....

thnx [1]