11For the 1st one, its A,C,D for sure....
Thinking abt B...not too sure.
D) for the 2nd qsn.
1) (Multiple Answers Correct)
An elliptical cavity is carved within a perfect conductor. A +ve charge "q" is placed at the centre of the cavity. Then-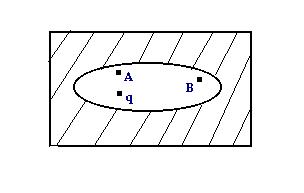
A) Elec. field near A = Elec. field near B (in the cavity).
B) Charge density at A = Charge Density at B.
C) Potential at A = Potential at B
D) Total Elec. Field Flux through the surface of the cavity is q/ε0.
2)Assertion-Reason Type
STATEMENT I- On going away frm a point charge or a small elec. dipole, elec. field decrease at the same rate for both the cases.
STATEMENT II- Electric field is inversely proportional to square of distance for a point charge.
A) Both correct, II explains I.
B) Both correct, II dosen't explain I.
C) I correct, II wrong.
D) I wrong, II correct.
E) Both wrong.
-
UP 0 DOWN 0 1 7
7 Answers
11
1D certainly for 2(field inversely proportional to r3 for dipole and r2 for point charge).
A,C,D for 1?
not confident about B
11Ans 1) C, D
Under electrostatic conditions , all points lying on the conductor are in the same potential. Therefore, potential at A= potential at B.
Frm Gauss's theorm, total flux through the surface of the cavity will be q/ε0.
13Fr#1 - [In Qn1 - A & B are ON the Cavity surface.] [1]
So, the answers given are- 1)C,D ...2)C
.... Wht i start with is- In the +nce of an external elec. field, charges arrange themselves in such a way tht net field inside the conductor is Zero.
Then, how can there be any net flux coming out thro' the cavity ?
1yeah but ur talking about a Solid conductor..in the given case..where it is hollow at a certain part(the cavity), there is a net flux
D is a right answer..but why C??
13Yep, it will be D) only, answer given is wrong, so v shouldn't confuse ourselves over this... [1]