1I wish we also had Centre of Charge...:)
Identical thin rods of length 2a carry equal charges,
Q, uniformly distributed along their lengths. The
rods lie along the x axis with their centers separated by
a distance of (in Fig. ). Show that the magnitude
of the force exerted by the left rod on the right
one is given by
F = (kQ2 / 4a2) ln ( b2 / b2 - 4a2 )
-
UP 0 DOWN 0 0 2
2 Answers
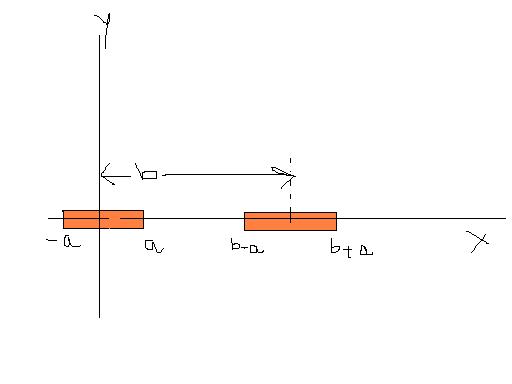
1find field due to the left rod at a distance r from its centre...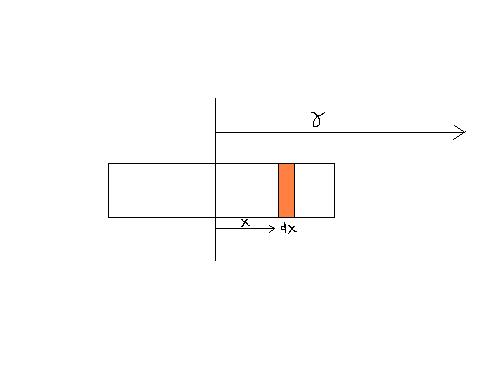
so E = ∫kλdx2a(r-x)2, where λ = Q/2a
integrating from -a to +a,
E = kQr2 - a2
So now coming to question the force on the right rod due to first,
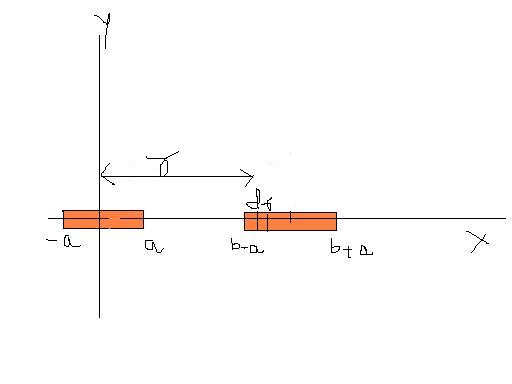
F = ∫(kQr2 - a2) λdr
now integrating (with r as variable) from b-a to b+a,
F = kQ24a ( log bb+2a - log b - 2ab )
which gives, F = kQ24a logb2b2 - 4a2
