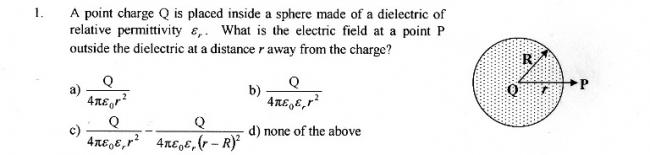71In second one, I'm a bit confused. Why would the empty region between the plates contain the charge. Charge is residing on the shells na?
16 Answers
71
11st one is (C) because the dielectric will cancel some amount of electric field due to Q.
12nd one A,B,C,D all match with III uncharged!
If the spheres are continuous!
2621. answer given is none of these.
2. i think the question is somewhat unclear
71For One: How could this be... I was pretty much sure of it.. Anyways let me digg some more or wait for an expert comment.
1for first one...i think..it shud be D
cant be A coz wen theres a region of dielectric...the electric field reduces a bit...option A wud hav been correct wen there was no region of dielectric
cant be B coz at a distance "r"...relative permittivity bears no significance coz its a free space region
cant be C coz of the same reason as B
hence D shud be the ryt one....
71I consider that to be a Lame reasoning.
" the electric field reduces a bit "
How does it reduce it and by how much.
" relative permittivity bears no significance "
If it reduces the Electric field then why it bears no Significance.
21I think vivek is correct
apply alternate form of gauss law
∫kE.ds = Qfree/ε0
1well vivek...yes its a bit lame reasoning for A bt not really for B n C
for B n C...luking at the question....the region with the dielectric ends at R...bt in options...its given upto r...
even i was a bit speculative abt A...
bt for B n C its pretty sure...coz at point "P"...relative permitivity really bears no significance at all...its a region of free space ryt??
1let us consider that we have a dielectric medium of relative permitivity k
let two charges be there of magnitude Q1 and Q2 , seperated by a distance r.
the force between the two charges inside the dielectric is given by:
F =Q1Q24πkε0r2
If we remove the dielectric , then we can consider the 2 charges to be placed in vacuum and seperated by a distance D
If the force acting between them remains the same,
=Q1Q24πε0D2 =Q1Q24πkε0r2
=> D= r√k
Thus we can keep two charges in vacuum at a distance r√k, which is equivalent to placing them a distance r apart in a dielectric.
Using this in the given question,
D=R√k + r-R
Thus the electric force between the two two charges is
F = Q1Q24πε0(R√k-R +r)2
Divide by Q2 to find the field and the answer comes out to be (D)
71Vikrant! don't know why I'm not satisfied with your one!
1@Vivek , why , in this answer i have effectively removed the dielectric , for making it easier to solve mathematicaly, though i agree that i am not able to solve this question by using gauss' law, but still i believe my answer is correct , i would appreciate if someone solved it using gauss' law!!