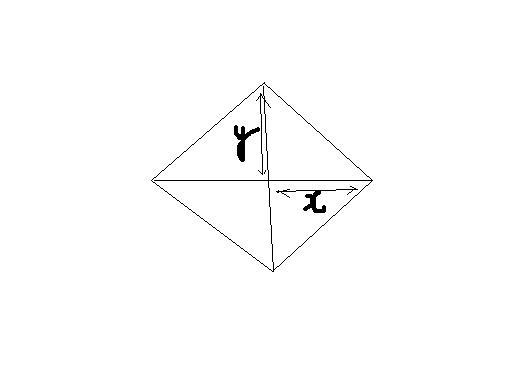
e=(Lucos2@/2sin@)B
In the figure, there is a square of side 'l'.
Ends C and D are pulled with velocity u. Find the induced emf at the instance when angle ABD is θ. Magnetic field is into the plane of paper.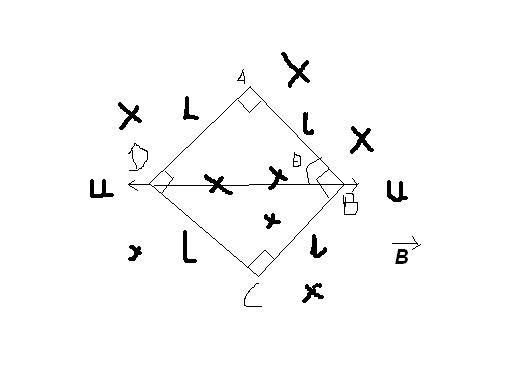
-
UP 0 DOWN 0 1 4

4 Answers
iitimcomin
·2009-07-31 19:56:19
-d(phi)/dt = -B dA/dt = -B d(2*1/2(2Lcos@)(Lsin@))/dt
d(Lcos@)/dt = u => d@/dt = -u/Lsin@
B[L2cos2@/2(u/Lsin@)] = e(induced)
B[L2ucos2@/2Lsin@] = e
(Lucos2@/2sin@)B
aposlil
·2009-08-01 05:46:07
εind= -d(B2xy)/dt
= -d(2Bx√l2-x2)/dt
Differentiate and put dx/dt= u and x=lcosθ