nice .You have failed me.
Suppose a disc of radius a placed on the ground with uniform surface charge density s with its axis vertical.A charged particle is dropped from a height H from the ground along the axis of the disc.Initially the particle is at rest so initial kinetic energy is equal to zero.Then see the point when the electric force on the particle is equal to the gravitational force.At that point velocity of the particle is zero.Hence the change in kinetic energy is equal to zero.So the work done by the net external force should be zero.But the resultant force is causing a net displacement in the downward direction.So there has to be some work done by the net external force.Please explain this.
-
UP 0 DOWN 0 0 67

67 Answers
You should hold a hundred kg mass and just apply a force of 900 Newton on it in the upward direction.Slowly increase the force to 1000 N then will the mass be not at rest?You are saying that it will not at rest.It may be possible in your world.But it is not possible in this world.
I have proved that net work done is not equal to zero.And one doubt from you all is that you all are considering it to be an SHM.If it is an SHM,then can you show me the other extreme positions?And you all say that this is the point of equilibrium where all forces add to zero and velocity is not equal to zero.Then will the particle still fall down?It was coming from top and it reached the point of equilibrium.Then it should move further from that point.But as it will move E(x) will increase over mg so net accelration will be upwards so it will go in the upward direction.One question you will ask that the velocity of the particle is downwards but the accelearation is upwards.
Suppose a car is acclerating on a rough surface with accelration a.What will happen will tha car not stop when its accelration will become equal to zero.Or will you say that the car will be performing SHM.
Now my proof that velocity of the particle will be zero is as follows:
What is the net force on the particle?
F=mg-qE(x)
Where E(x) is the electric field due to the disc.
From Newton's Second Law of motion
ma=mg-qE(x)
=>a=g-qE(x)/m
Velocity of the particle is given by
v=(g-qE(x)m)t............(1)
At the point of equilibrium
mg=qE(x)
g=qE(x)/m...........(2)
Keep on calculating wih me.
Then from equations(1) and (2)
v=0.
Oh your brain!How bad is that!
Any question upto this point then let me know.
I think it is not my doubt but your doubt.
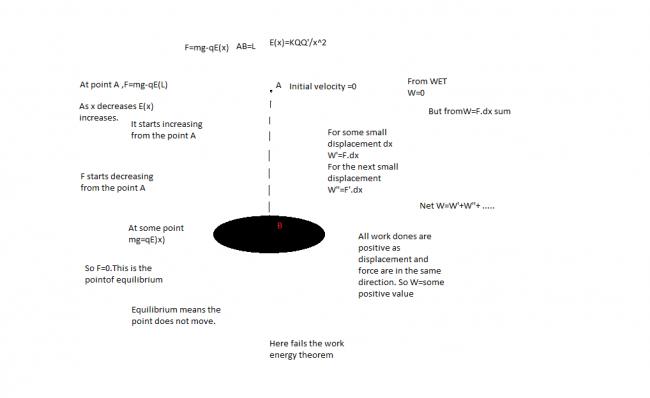
Do not talk about that case here.Are here not forces?Are you blind?Force and displacement means work done.And yes if you still find mistake in me, please see the given figure. I think nobody has seen that yet.And also if you think the final velocity is not zero then prove it not to be equal to zero.Nobody has yet been able to prove that.I say prove in this case.Not in any other case.What did I say?In this case not in the other cases.And that nobody has proved yet.Please feel free to say anything from you about me.
displacement doesnt guarantee work done , a particle travelling with constant velocity also gets displaced , will you say work is done here ???
For those who do not agree with my statement that when there is some displacement then there is some work done should check this link:http://www.physicsclassroom.com/class/energy/u5l1a.cfm And I think that is a very useful link to tell you that.
it may ,might or may not mean.But tell me in this case how is it not zero?
How can you prove that equilibrium does not mean that particle is at rest.
EQUILIBRIM DOENT MEAN PARTICLE IZ AT REST...???HV U HEARD DYNAMIC EQUILIBRIM
Then see the point when the electric force on the particle is equal to the gravitational force.At that point velocity of the particle is zero
THIS IS PURE BLL SH*T...........HW THE HELL CAN VELOCITY B ZERO WHEN FORCES ARE EQUAL.......THE NET FORCE IZ ZERO BUT PARTICLE WUD STILL MOVE AS IT HAZ MOMENTUM...!
hey vinay brush ur cocepts study force analysis ....ur que isnt clear at least write one equation or even a doagram....talking in air >??????
Let us not bring t anywhere
From Newton second law
ma=mg-qE(x)
a=g-qE(x)/m
vdv/dx=g-qE(x)/m
v2/2=gx-q(int.)E(x)dx/m
At equilibrium
g=qE(L')/m
v2/2=qx(E(L'))/m-q(int.)E(x)dx/m
.
Integrate it from ∞→L'
Yaaaaaaa it is not equal toE(L')
Hence velocity is not equal to zero.
Fine.So WET is still valid
I think this is the biggest discussion held on the internet for doubts.
I was not able to reply to you.
Ok. Let the particle covers a displacement dx for that W1=fdx.Then for next dx we have W2=f'dx.And keep on doing like this then Net W=W1+W2 +...Now how can you prove W to be equal to zero.
I think you are referring to your post #7
When you drop the particle from a very high point where there is no electrostatic force acting, the particle starts gaining kinetic energy tilll it reaches a max. value.....the work done by net external force is positive upto this point.......now there will be a repulsive force which starts decreasing its velocity/kinetic energy.Here the net force is in upward direction (as the velocity decreases). So from now onwards the work done will be negative. There comes a point where the body loses its entire kinetic energy. This point is not necessarily the equilibrium point. It is infact lower than it (because the particle crosses it equilibrium point with some K.E.). From work energy theorem, change in K.E.=0 so Sum of the work done by external forces at infinitesimal displacements upto that point equal 0.
I think that the particle executes SHM here.
EDIT: I see that Eminem cleared your doubt.
Ok!Thank you for all!I will come with my more doubts.Good bye!Good night!
no it is ok, no one is bad or good , bad or good is relative,
every one makes mistakes, and i make the silliest mistakes, you should be relieved that this concept of yours is clear now !!
and one more thing the electric field that you wrote in that picture is incorrect , that electrc fled too will have to be found out by integration, you cant assume the disc as a charged particle unless dyou want to calculate electric field a tsome long distance