isnt the ans zero....
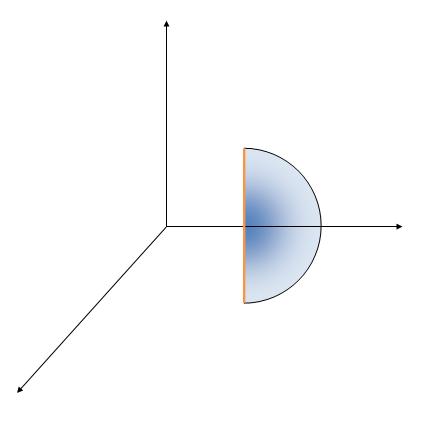
A point charge q is placed at origin. Calculate the electric flux through the open hemispherical surface : (x-a) 2 + y2 +z 2 = a 2 ,
x ≥ a.
-
UP 0 DOWN 0 1 9

9 Answers
You will need the concept of solid angle...
I am not sure if you would want to use that for jee!!
yups u have to use solid angle...and i believe taht its a concept u shouldnt miss for JEE
The solid angel here is ω
which is given by 2π(1-cosθ)
here θ=π/4
so ω=2Ï€(1- 1/√2)
Now flux through this section of solid angle ω will be \frac{\omega }{4\pi}\frac{q}{\varepsilon _o}=\frac{2\pi(1- 1/\sqrt{2})}{4\pi}\frac{q}{\varepsilon _o}=\frac{q}{2\varepsilon _o}(1-\frac{1}{\sqrt{2}})
the base of the hemisphere will be the x-y plane,
and all the flusk entering the sphere will leave from the other side....
hence the net flusk will be zero...
i dont know weather this is right... but well lesee.
karan u r going wrong in ur concept sumwhere.eurekas got it right...u will ahve to use solid angle..:)
The solid angle is not necessary though. You could simply calculate the flux through the flat base of the hemisphere.