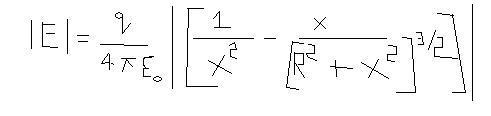1
1if one studied PROPERTIES OF INFINITY or rather it is a physics question so let me say the PROPERTIES OF FAR_OFF.....he will answer this one IMMEDIATELY!
INFINITY/FAR_OFF IS A BOUNDLESS LARGE VALUE OF x....u choose a 106 units for x there still exists a LARGER VALUE!!!!!!!!!!!!!!
so,firstly let me give the BOGGGGGGGGUSSSSS SOLUTION![i.e. THE WRONNNNNNNNNGGGG SOLUTION]
BOGUS SOLUTION
so using the formula of case 2 and the formula for field of a point charge one concludes II E II =0 which is wrong
why wrong?? the case-2 is BETTER SAID NEVER ACHIEVED IN REALITY......watever be the case u choose one x and u get another higher x......so using FORMULA GIVEN BY MR>ATGS TO SOLVE THIS ONE NA D CONCLUDE THT IIEII=0 is a BOGUS ACT!
now coming to TRUE SOLUTION:
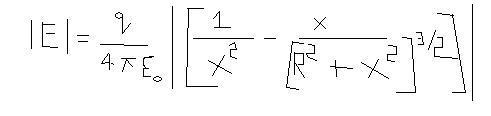
 49
49ahem!!
right!! that was just to confuse!!
neways here comes the actual answer!!and that too latexified!!:P
E= \frac{q}{4\pi \epsilon _{o}}[\frac{1}{x^2}-\frac{x}{(R^2+x^2)^{3/2}}]=\frac{q}{4\pi \epsilon _{o}x^2}[1-\frac{x^3}{(R^2+x^2)^{3/2}}]
=\frac{q}{4\pi \epsilon _{o}x^2}[1-\frac{1}{(1+\frac{R^2}{x^2})^{3/2}}]=\frac{q}{4\pi \epsilon _{o}x^2}[1-{(1+\frac{R^2}{x^2})^{-3/2}}]
now since R2<<x2,
so, R2x2<<1
so expanding (1-R2x2)^(-32) binomially we can ignore higher powers of R2x2
so,
E=\frac{q}{4\pi \epsilon _{o}x^2}[1-{(1+\frac{R^2}{x^2})^{-3/2}}]=\frac{q}{4\pi \epsilon _{o}x^2}[1-(1-\frac{3}{2}.\frac{R^2}{x^2})]=\frac{3qR^2}{8\pi \epsilon _{o}x^4}
 1
1yaar latex use karne ka man nahi hota mera![3][3][3]............
NEVER EVER IN HISTORY HAS ANAND GUPTA USED LATEX ON TIIT!!!!![4]