simplification
:
v = ÏPvoÏP + B2lvo
lets take it to another level :P
A horizontal rectangular plastic pipe of width w and height h, which closes upon itself, is filled with mercury of resistivity Ï. An over pressure P is produced by a turbine which drives this fluid with a constant speed vo. The two opposite vertical walls of a section of the pipe with length l are made up of copper.
The motion of a real fluid is very complicated. To simplify the situation we assume the following:
Although the fluid is viscous, it's speed is uniform over the entire cross-section.
The speed of the fluid is always proportional to the net external force acting upon it.
The fluid is incompressible.
The copper walls one electrically shorted externally and a uniform, magnetic field B is applied vertically upwards only in this section.
The base of the pipe is kept in the x-y plane..the length l is along x-axis,width w along y axis and height h along z axis.
a) Find the force acting on the fluid due to the magnetic field(due to L, B, h, w, Ï and new velocity v)
b) Derive an expression for the new speed v of the fluid (in terms of vo, P, L, B and Ï) after the magnetic field is applied.
c) Derive an expression for the additional power that must be supplied by the turbine to increase its speed to the original value vo.
d) Now the magnetic field is turned off and mercury is replaced by water with a speed of vo. An electromagnetic wave with single frequency is sent along the section wire length L in the direction of the flow.
The refractive index of water is n and vo << c.
Derive an expression for the contributing of the fluid's motion to the phase difference between the waves entering and leaving the section L.
(Now that is what i call a superposition of chapters. :D)
not a doubt ;)
i am giving the approximate figure that i drew in paint!! :D
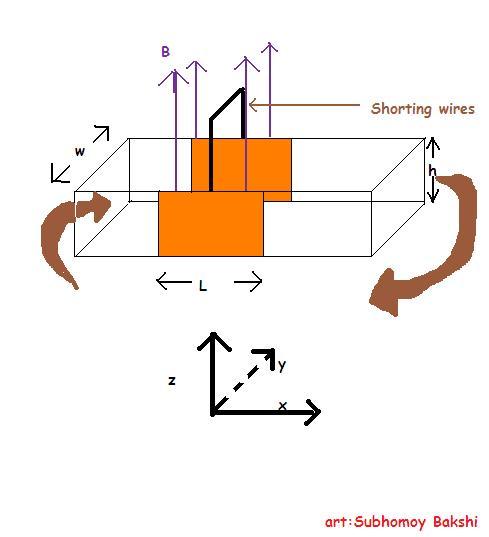
hope u all like the image :P
had to work a lot to get it according to the question :P
i have an unfathomable desire to post solution... am doin the same nw!
a) Consider the section of mercury flowing past the copper walls of length l, height h, breadth w)
as a hint i had already included that in the figure!
consider any single (free) electron in this volume section.
velocity is vx i.
magnetic field exerts a force on it
Fb = -e [vx X Bz] = -evB
this results in accumulation of electrons to the other end of the tube as seen from this end hence motional emf is created across this end..
motional emf=V
thus work done in moving the electron W=eV
but the work done can also be expressed as W=Fy.w=evB.w
thus, eV=evBw
or, V=vBw
resistivity given is Ï
so resistance of this volume is Ï.length/area so, R=(Ï x w)/(l x h)
so current in mercury..
i=V/R = vBw.lh/ÏBw = Bvlh/Ï
this clearly flows in -j direction (negative y) since the positive end is closer to us as seen from out of the computer screen side!!
so force is
i x (lxB)=(Bvlh/Ï)xBw(-j x z) = -(B2wvlh/Ï)i !! [1]
first part solved!! [1]
b)
initially total force on the fluid was Pressure x area, i.e. Phw
and initially velocity was vo
also it says velocity is proportional to the force
thus, vo = K.Phw
K=vo/Phw
now net force= Phw - (B2hwlv/Ï)
new velocity v=K.[Phw - (B2hwlv/Ï)] = vo[Phw - (B2hwlv/Ï)]Phw = vo{1-B2lvPÏ}
v=vo{1-B2lvPÏ}
now please someone simplify from here...
b)
initially total force on the fluid was Pressure x area, i.e. Phw
and initially velocity was vo
also it says velocity is proportional to the force
thus, vo = K.Phw
K=vo/Phw
now net force= Phw - (B2hwlv/Ï)
new velocity v=K.[Phw - (B2hwlv/Ï)] = vo[Phw - (B2hwlv/Ï)]Phw = vo{1-B2lvPÏ}
v=vo{1-B2lvPÏ}
now please someone simplify from here...