1i dont agree wid aveek nd his method......especiaallly cant understand how u got total charge on the ring = 2 λ0 R
A semicircular ring of mass m is kept in x-y plane with centre at origin.It
is charged in such a way such that charge/unit length varies as λ=λocosθ .
Find accelration of ring when electric field E=Eoxi+Eoj is switched on.
-
UP 0 DOWN 0 0 17
17 Answers
1
49well i gave another question!!!
A semicircular ring of mass m is kept in x-y plane with centre at origin. It
is charged in such a way such that charge per unit length varies as λ=λocosθ (θ is angle measured w.r.t. positive x-axis!).
Find torque about the centre of ring when electric field E=Eoxi+Eoj is just switched on.
49Let me try this...
the applied field= Eoxi + Eoj
so constant field applies to y direction, and by symmetry will exert NO NET FORCE on the half ring of charge...
so the applied field is equivalent to Eo . x . i only!!
referring to Sanchit's diagram,
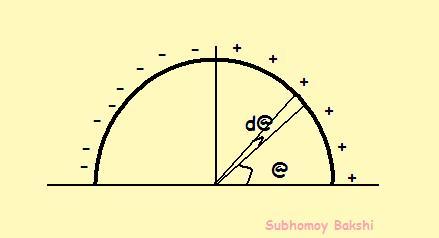
considering a small arc subtending angle d@ as in figure, and consider the charge distribution is uniform in this region...
length=Rd@
linear charge density=λ=λocos@
so charge on the small element=Rλocos@d@
x coordinate=R cos@
so, field=EoRcos@
so force on small element = EoλoR2cos2@d@
so net force=\int_{0}^{\pi }{E_o \lambda _oR^2cos^2\theta d\theta }=\frac{E_o \lambda _oR^2}{2} \int_{0}^{\pi }{(cos2\theta+1) d\theta} = \frac{E_o \lambda _oR^2}{2}.\left[0+\pi -0-0 \right]=\frac{\pi E_o \lambda _oR^2}{2}
thus, acceleration=\frac{\pi E_o \lambda _oR^2}{2m}
1@ Sanchit : Yup this was a mistake :
following ur own figure :
the charge distribution : charge is located at the ends of the wire and not the upper part.....
as charge at the ends = λ0 and charge on top = 0
so by symmetry the centre of charge will lie on the lower end of the axis of the semicircular wire . as this is a point charge where the entire charge is concentrated look at the field vector :
in x direction acceleration is ax = qE/m
and in y direction acceleration is once again the same as
→ →
a = q E / m
1yaar shudnt it be like this:::::
dq = λ dl
dq = λ0 cosθ R dθ
Ï€
Q = λ0 R ∫cosθ dθ
0
Q=0
1dq = λ dl
dq = λ0 cosθ R dθ
Ï€/2
Q = 2 λ0 R ∫cosθ dθ (by symmetry)
0
so Q = 2 λ0 R
....i think this clears ur doubt.
1"in x direction field will be perpendicular to the charge .... hence accn. = 0" can u explain... how field ll be prependicular to the charge????????
1not sure of the answer..i'm getting : ( 2√2 λ0 R E0 )/m
Now if ajoy is not speaking of a unform field...i can't say anything more than the thing that my entire process is wrong...........
@ Kaymant Sir : Isn't he trying to say that the field in the X-direction will vary with x ?
1also note that the total charge on the ring is constant above.
1i think he has made the mistake with this x thing in the expression.
else as far as i can say :
total charge on the ring = 2 λ0 R
where R is the radius
now there is a centre of charge where the entire charge is concentrated.........we can work out from this :
in x and y - both dir. apply a= qE/m
I think this can be the method...........(not so sure)
66Are you sure about the given field? It seem dimensionally inconsistent.
1i will try and post the solution....it seems a bit tricky...
1I know that,but I'm not getting how to apply that in the problem.
Pleae post at least 60 percent of soln.....