How does it move.

sir post ur method pls and also tell the mistake in abv approach

i think its time to open up the ans to this Q :)

celestine, even in the polar form you should not get such a horrible equation.

but i am getting it !

also can u justify #13 and tell why #12 is wrong ?

sir i request u to post final ans and hide it

i want to cross check

The charge will move to and fro in a semicircular path, very much like a pendulum with its suspension at the origin.

ok that means #12 is true only

wow a semicircular path !

ok sir im workin on derivin that

I said that the last line in #12 is not correct.

celestine... did u come up with something?

ok sir i will post my long derivation of # 18

in few minutes

i m using polar form

Z = rsin@
X= rcos@

d²Z/dt² = kcos@/r³

d²X/dt² = -2ksin@/r³

from abv

ksin2@/2r³ = (d@/dt)²r - d²r/dt²

k(1+sin²@)/r³ = 2r.dr/dt.d@/dt + rd²@/dt²

solving further i got #18

but puttin dr/dt =0 in abv eq im gettin a contradiction

so i assume my eqs are wrong ,but where is it wrong ?

note:

d²(rsin@)/dt²
= 2dr/dt .d@/dt cos@ + d²r/dt²sin@ + d²@/dt². rcos@ - (d@/dt) ² rsin@

d²(rcos@)/dt²
= 2dr/dt .d@/dt(-sin@) + d²r/dt²cos@ + d²@/dt².(- rsin@) - (d@/dt) ² (- rcos@)

well, the ques is interesting

but

i think that the motion that the charge will undergo should be oscillatory.( to and fro)..

do tell how u ppl are getting curved paths!...

and sir also tell how u hve kept the dipole? ( is its midpoint at the origin???, i think it should be ).....

Celestine, your mistake in #26 lies at the very beginning. You see d²z/dt² is the acceleration along the z axis. So the correct equation should be
\dfrac{\mathrm{d}^2z}{\mathrm{d}t^2} = \dfrac{q}{m}(E_r\cos\theta -E_\theta \sin\theta)
and similarly for the second equation.
Here, \theta is measured from the direction of the dipole itself as shown below: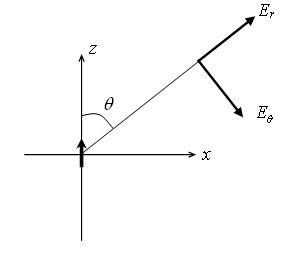

Apart from considering the force equations, we could take up the conservation laws. First of all, since the point charge is released on the xy plane, we could as well take it to be released from the point (R,0,0) itself. Thus, the initial potential energy is zero since for a dipole the potential is
V_\mathrm{dip} = \dfrac{p\cos\theta}{4\pi\epsilon_0 r^2}
and here \theta = 90^\circ. Also, the initial kinetic energy is zero. Since the system is closed, we have from the conservation of energy that for all (r,\,\theta),
\dfrac{1}{2}mv^2+\dfrac{pq\cos\theta}{4\pi \epsilon_0r^2}=0 -------------- (1)
Since the k.e is always positive, the second term must be negative implying that \cos\theta\leq 0. This means that the point charge is constrained to move in the region \dfrac{\pi}{2}\leq\theta\leq \dfrac{3\pi}{2}
Again, the torque of the electric force about the origin is responsible for the changing the angular momentum of the point charge:
\dfrac{\mathrm{d}}{\mathrm{d}t}(mrv_\theta)=qrE_\theta =\dfrac{pq\sin\theta}{4\pi \epsilon_0r^2} -------- (2)
Now, noting that v^2=v_r^2 + v_\theta^2
we get from (1), that
\dfrac{1}{2}m((rv_r)^2 + (rv_\theta)^2)+\dfrac{pq\cos\theta}{4\pi\epsilon_0}=0
Differentiating w.r.t time, we get
\dfrac{m}{2}\dfrac{\mathrm{d}}{\mathrm{d}t}(rv_r)^2 + rv_\theta \dfrac{\mathrm{d}}{\mathrm{d}t} (mrv_\theta)-\dfrac{pq\sin\theta}{4\pi\epsilon_0}\dfrac{\mathrm{d}\theta}{\mathrm{d}t}=0
Using the fact that v_θ = r dθ/dt, we obtain from the above
\dfrac{m}{2}\dfrac{\mathrm{d}}{\mathrm{d}t}(rv_r)^2 + r^2\dfrac{\mathrm{d}\theta}{\mathrm{d}t} \dfrac{\mathrm{d}}{\mathrm{d}t} (mrv_\theta)-\dfrac{pq\sin\theta}{4\pi\epsilon_0}\dfrac{\mathrm{d}\theta}{\mathrm{d}t}=0
Dividing throughout by r², we get
\dfrac{m}{2r^2}\dfrac{\mathrm{d}}{\mathrm{d}t}(rv_r)^2 + \dfrac{\mathrm{d}\theta}{\mathrm{d}t} \dfrac{\mathrm{d}}{\mathrm{d}t} (mrv_\theta)-\dfrac{pq\sin\theta}{4\pi\epsilon_0r^2}\dfrac{\mathrm{d}\theta}{\mathrm{d}t}=0
But because of (2), the last two terms cancel, and we are left with
\dfrac{\mathrm{d}}{\mathrm{d}t}(rv_r)^2 =0
That means that
rv_r=\textrm{ constant}
Since initially the charged particle was at rest, so the constant is zero. Accordingly
v_r=\dfrac{\mathrm{d}r}{\mathrm{d}t}=0
which gives us
r=\textrm{ constant}=R
Hence, the particle moves in a semi-circular path located in the region \dfrac{\pi}{2}\leq\theta\leq \dfrac{3\pi}{2}.

hats off to u sirji..

very nice Q and Ans

oops sorry sir totally forgot abt this problem !!!!!!

tried only 5 mins and was going in the same direction .. should have continued ...

okay... find the equation of the trajectory.

rickde u shud replace y by z see Q

initially it will move in the -ve y axis direction then curve towards -ve x axis while continuing its motion along the y axis

Qualitatively i can say that its a bounded motion as

Mech energy = 0 initially

so PE <=0

it indirectly implies the charge is always in either -ve or +ve z axis as else PE wud change sign

the body goes to infinity? hmm... that's intereting.. how did u get that?

@celestine,
things should be quantitative

celestine how did u get that equation.........u wrote????.........u xplain it ...............i din read any such equation for dipoles...........

maybe even i know it without realizing....but as far as i think i don know how u got it.......so kindly xplain ur equation

ok sir

do u need qualitative or quantitative ans ?