Can someone prove that for a hollow sphere given a uniformly distributed charge Q and rotated with ang. vel. ω the magnetic moment of sphere =
(Q/3)* r2ω where r is radius
11Angular Momentum = L (let) = (2/3) mr2. ω
Magnetic Monent = M (let)
For any regular body with uniform mass & charge distribution rotating with ω :
M/L = Q/(2m) m : mass of body.
So,for this case,
M = Q((2/3)mr2. ω) / (2m) = (Q/3) . r2 ω
33u can do this by integrations... by assuming rings...
or M/L=q/2m
M is mag mom... L is ang momentum about COM... q is charge.. m is mass...
1@ rkrish
arre that's why i am asking the question
and u are underlining i don't know what
i asked for proof and this is not it
give me a proof for hollow sphere
@ abhi can u give me the proof
i have been tru all this b4 and i am asking bcozt i had problem with integration of those "rings" why don't u help me with that part
1anyone ....
i have problems in integrating this...
ok can someone prove the thing for any rigid body in general ??(if it is true for all that is)
33
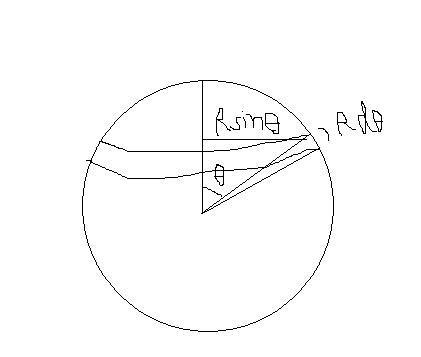
Charge on ring.. is Qsinθdθ
2
i=Qsinθdθω/2π
2
idA=Qsinθdθ ωπ(Rsinθ)2
2 2Ï€
M=∫idA
=QR2ω 2 0∫π/2sin3θdθ
4
QR2ω/3
1ok thanks i tried it three times but with no result somehow i was getting sin^4 there..
it must be ok .. anyway it was just curiosity u know..